使用教材:
清华大学电子学教研组编 . 杨素行主编 . 模拟电子技术基础简明教程 . 3版 . 北京:高等教育出版社,2006.
作业内容:
模电作业是这样的:
第六章可以做1 2 3 6 7 8题以及PPT上一题
5月8号前交
¶6-1 && 6-3
反馈的极性可以使用瞬时极性法判断:
交流负反馈的组态判断:
(1)从输出端的判别上分为电压、电流负反馈
使用交流短路法:将输出电压 $u_o$ 交流短路,分析反馈信号是否还存在
若反馈信号消失,则为电压负反馈,反之,则为电流负反馈
(2)从反馈信号与输入信号在输入回路中的叠加方式上分为串联、并联负反馈
若反馈信号与输入信号在输入回路中以电压形式求和,则为串联负反馈
若反馈信号与输入信号在输入回路中以电流形式求和,则为并联负反馈
简单的说,看反馈信号与输入信号在不在同一个端子上,异串同并
¶a
上图中共有四个反馈支路:
由 $R_F$ 和 $C_F$ 引回的级间反馈是交流正反馈
由 $R_{e1}$ 既引入了交流负反馈也引入了直流负反馈,其中交流负反馈的组态为电流串联负反馈
可以稳定本级工作电流,提高输入电阻
由 $R_{e2}$ 与 $C_e$ 引入的是直流负反馈(由于旁路电容 $C_e$ 的存在)
由 $R_{e3}$ 既引入了交流负反馈也引入了直流负反馈,其中交流负反馈的组态为电压串联负反馈
可以稳定输出电压,提高本级输入电阻,降低输出电阻
¶b
上图中共有四个反馈支路:
由 $R_F$ 引回的级间反馈既有交流负反馈也有直流负反馈,且交流负反馈的组态为电流串联负反馈
可以稳定输出电流,提高输入电阻
由 $R_{e1}$ 既引入了直流负反馈也引入了交流负反馈,其中交流负反馈的组态为电流串联负反馈
可以稳定本级工作电流,提高输入电阻
由 $R_{e2}$ 与 $C_e$ 引入的是直流负反馈(由于旁路电容 $C_e$ 的存在)
由 $R_{e3}$ 引入了交直流负反馈,其中交流负反馈的组态为电流串联负反馈
对本级作用与 $R_{e1}$ 相同
以(b)为例,说明一下瞬时极性法的使用步骤:
首先,不妨设输入端的正极性端有一个瞬时的电压正增量
那么就会引起 $VT_1$ 管的基极电压出现一个正增量,从而引起 $VT_1$ 管有一个向下的电流增量
使得发射极电位有一个正增量,可判断 $R_{e1}$ 所在支路引起的是本级的负反馈
集电极电位出现一个负增量,使得 $VT_2$ 管的基极电位有一个负增量
$VT_2$ 管是一个PNP型的管子,分析方法与NPN管类似
由$VT_2$ 管的基极电位负增量引起由发射极向集电极方向的电流增量
使得发射极电位出现一个负增量,可判断 $R_{e2}$ 与 $C_e$ 所在支路引入的是本级的负反馈
集电极电位出现一个正增量
于是 $VT_3$ 管的情况与 $VT_1$ 管的情况一样,发射极电位出现一个正增量
即 $R_{e3}$ 引入了本级的负反馈
$R_F$ 所在支路使得 $VT_3$ 管发射极的正增量影响到 $VT_1$ 管的发射极又有一个正增量
于是 $R_F$ 所在支路引入了级间的负反馈
¶c
上图中共有三个反馈支路:
由 $R_F$ 引回的级间反馈是交直流负反馈,且交流负反馈的组态为电流并联负反馈
可以稳定输出电流
由 $R_{e1}$ 引入了交直流负反馈,其中交流负反馈的组态为电流串联负反馈
可以稳定本级工作电流,提高本级输入电阻
由 $R_{e2}$ 与 $C_e$ 引入的是直流负反馈(由于旁路电容 $C_e$ 的存在)
¶d
上图中共有两个反馈支路:
由 $R_F$ 引回的级间反馈是交流负反馈,其组态为电压并联负反馈
可以稳定输出电压,降低输出电阻
由 $R_{e1}$ 引入了交直流负反馈,其中交流负反馈的组态为电流串联负反馈
可以稳定本级工作电流,提高输入电阻
¶e
上图中共有两个反馈支路:
由 $R_F$ 引回的级间反馈是交直流负反馈,其中交流负反馈的组态为电压串联负反馈
可以稳定输出电压,提高输入电阻,降低输出电阻
由 $R_{e3}$ 引入了交直流负反馈,其中交流负反馈的组态为电流串联负反馈
可以稳定本级工作电流,提高本级输入电阻
¶f
上图中共有两个反馈支路:
由 $C_3$ 与 $R_b$ 引回的本级反馈为交流正反馈(电压并联)
由 $R_e$ 引入了交直流负反馈,其中交流负反馈为电压串联负反馈
即射极输出器本身的电压串联负反馈,故有稳定输出电压,提高输入电阻,降低输出电阻的作用
其实 $C_3$ 还有一个作用呢qwq
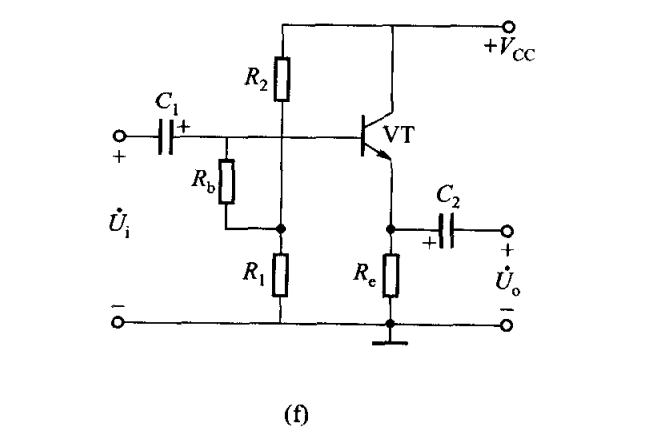
如果没有接电容 $C_3$ ,如上图所示,可知其输入电阻约为:$R_i=R_b+R_1//R_2$
(即忽略基极电流)
现由$C_3$ 与 $R_b$ 引回一个交流正反馈,由其交流通路:
在中频段时,电容 $C_3$ 可视为短路,则电阻 $R_b$ 两端电压约为 $\dot U_i-\dot U_o$
则流过电阻 $R_b$ 的电流约为 ${\dfrac {\dot U_i-\dot U_o}{R_b}}$
忽略基极电流,则可将流过电阻 $R_b$ 的电流视为输入电流
则可求得输入电阻为:$R_i={\dfrac {\dot U_i}{\dot I_i}}={\dfrac{\dot U_i}{\dfrac {\dot U_i-\dot U_o}{R_b}}}={\dfrac {\dot U_i\cdot R_b}{\dot U_i-\dot U_o}}$
又由于该电路为射极输出器电路,其电压放大倍数近似于 $1$ ($<1$)
即其基极电位与发射极电位近似,有:$\dot U_i\approx \dot U_o$ 那么则有:$R_i\to\infty$
大大地提高了其输入电阻
这种方法又称为“自举”:将输出电压通过电容引回到输入回路以提高输入电阻
可通过看书上 例6.4.3 加深理解
¶6-2 && 6-3
¶a
正反馈
(正反馈也有组态的吗? 如果有的话,这里应为电压并联吧)
¶b
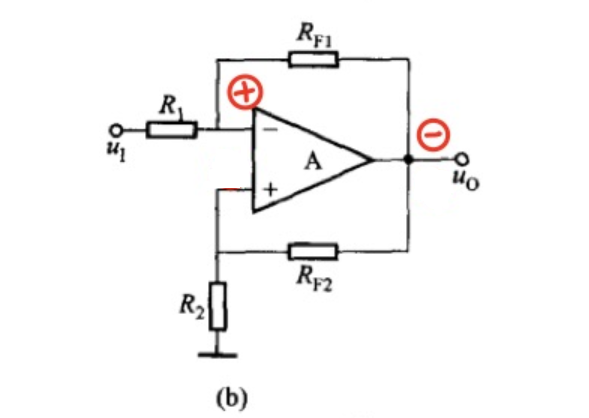
由 $R_{F1}$ 引入的是电压并联负反馈
可以稳定输出电压,降低输出电阻
由 $R_{F2}$ 引入的是正反馈(电压串联)
¶c
电压并联负反馈
可以稳定输出电压,降低输出电阻
¶d
电流串联负反馈
可以稳定输出电流,提高输入电阻
¶e
电压串联负反馈
可以稳定输出电压,提高输入电阻,降低输出电阻
¶f
电流并联负反馈
可以稳定输出电流
¶6-6
由题意可知,其临界状态为:
${\dfrac {\mathrm{d}A_f/A_f}{\mathrm{d}A/A}}={\dfrac {1}{25}}$因为有:${\dfrac {\mathrm{d}A_f}{A_f}}={\dfrac {1}{1+AF}}\cdot {\dfrac {\mathrm{d}A_f}{A_f}}$
则可知:${\dfrac {1}{1+AF}}={\dfrac {1}{25}},1+AF=25,AF=24$
又有:$A_f={\dfrac {A}{1+AF}}$
故:$A=(1+AF)A_f=25\times 100=2500$
$F={\dfrac {24}{2500}}=9.6\times 10^{-3}$¶6-7
由题意可知:
$\dot A_{um}=-100 \ \ \ \ f_L=30Hz\ \ \ \ f_H=3kHz\ \ \ \ \dot F_{uu}=-10\%$那么则有:
$\dot A_{uf}={\dfrac {\dot A_{um}}{1+\dot A_{um}\dot F_{uu}}}={\dfrac {-100}{1+(-100)\cdot(-0.1)}}\approx -9.09$$f_{Lf}={\dfrac {f_L}{1+\dot A_{um}\dot F_{uu}}}={\dfrac {30}{11}}Hz\approx 2.73Hz$
$f_{Hf}=(1+\dot A_{um}\dot F_{uu})\cdot f_H=11\times 3kHz=33kHz$
¶6-8
啥都不用管,先整上瞬时极性法
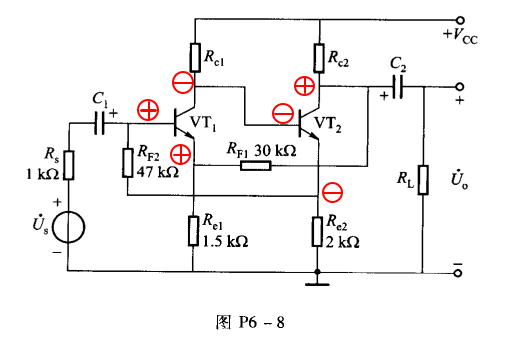
(1)
共有两条支路为级间反馈:
由 $R_{F1}$ 引入电压串联负反馈
由 $R_{F2}$ 引入电流并联负反馈
又有两条支路为本级反馈:
由 $R_{e1}$ 和 $R_{e2}$ 分别引入电流串联负反馈
(2)
接一个隔直电容 $C_{F1}$ 与 $R_{F1}$ 串联
再接一个旁路电容 $C_{F2}$ 与 $R_{F2}$ 并联
(3)
$C_{F1}$ 与 $R_{F1}$ 引入的交流电压串联负反馈可以稳定输出电压,提高输入电阻,降低输出电阻
$C_{F2}$ 与 $R_{F2}$ 引入的直流负反馈可以稳定各级Q点
(4)
若满足深度负反馈条件
则电压放大倍数可如此估算:
$\dot A_{uf}={\dfrac {1}{\dot F_{uu}}}=1+{\dfrac {R_{F1}}{R_{e1}}}=21$
¶附加题
PPT上一题
瞬时极性法判断正负反馈与组态
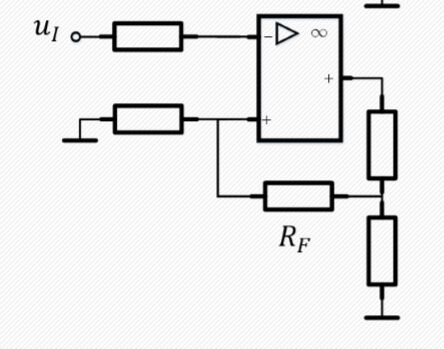
正反馈
如果有组态的话,我想应该是电压串联
附:如果做完了前边的题就一定感觉到了这是道水题(手动狗头)
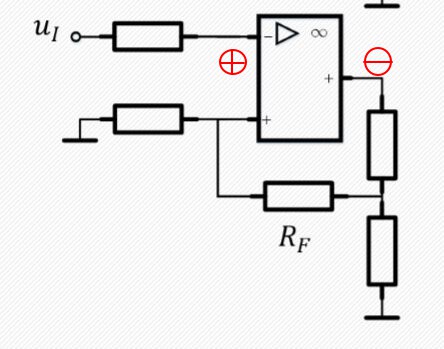
¶附图:分立元件反馈判定
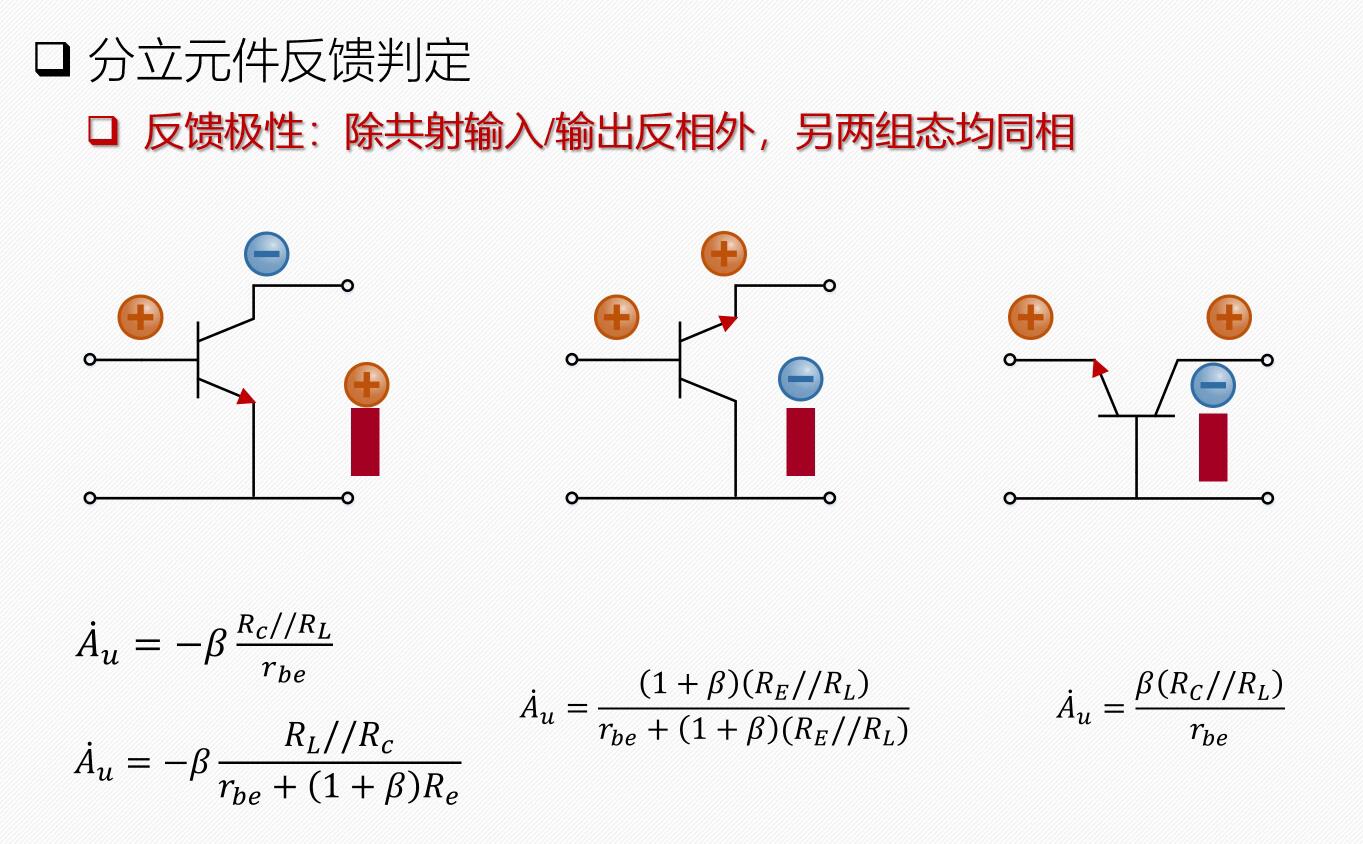
参考文献:
模拟电子技术基础简明教程第3版及其教学指导书

