¶一、前言
在我校开展科研选题的背景下,我小组决定对四旋翼飞行器的控制进行研究,并确定课题名称为“基于STM32的四旋翼飞行器控制系统的研究”, 开始对飞行器的软硬件系统以及控制逻辑进行系统化的学习。
其中,我主要参与学习了对四旋翼飞行器的飞行原理与姿态解算的分析,现撰写报告如下。
¶二、概述与发展现状
¶1. 概述
四旋翼无人机广泛应用于民用与军事领域,例如救援、侦察、勘探等方面,其主要优点如下:
- 机械结构简单
- 飞行姿态稳定
- 易于小型化和微型化
- 可执行的任务多样化
- 成本低、噪声小、易于维护
¶2. 发展现状
到2012年左右,国际上普遍认为四轴飞行器的控制已经不再是学术研究问题,而是成熟的技术。学术研究的方向也转向了基于四轴飞行器做智能导航或者多飞行器的编队控制。
四轴飞行器的智能导航指的是利用机器视觉技术、人工智能技术让四轴飞行器能像人一样在复杂环境中活动。
多飞行器的编队控制是指同时控制多个飞行器,或者让多个飞行器自主编队飞行。
¶3. 技术关键
¶3.1 总体设计优化
设计微小型四旋翼飞行器时,原则上希望达到以下几个方面的要求:
即质量轻、尺寸小、速度快、能耗与成本低,但这几者之间存在相互制约与矛盾,于是要求设计者综合考虑,不断对方案进行优化。
¶3.2 能源动力系统
能源动力装置包括了旋翼(螺旋桨)、微型直流电机、电调、机载电池等,其质量占了整个机体质量的很大部分,需要选用更轻、更高效的能源动力装置。
¶3.3 建立数学模型
机体在飞行过程中受到多种物理效应的作用(空气动力、重力、陀螺效应和旋翼惯量矩等),且容易受到气流等外部环境的干扰,这些都给建立有效、可靠的动力学模型带来了困难。同时,微型飞行器空气动力学特性与常规飞行器有很大的不同,需要了解新的理论与研究手段。
¶3.4 飞行控制
四旋翼飞行器是一个具有六自由度(位置与姿态)和四个控制输入(旋翼转速)的欠驱动系统,具有多变量、非线性、强耦合和干扰敏感的特性,且传感器性能会受到模型准确性与传感器精度的影响,需要精确控制飞行器姿态,具有较强的抗干扰与环境自适应能力。
¶3.5 定位、导航与通信
近地面环境地形复杂、干扰源多,对定位系统、导航技术与通信链技术的可靠性、安全性与抗干扰性有着较高的要求。
¶三、基本飞行原理
¶1. 概述
四旋翼飞行器是一个 欠驱动系统(Underactuated System),即其控制自由度小于其活动自由度的系统,其拥有六个 活动自由度 ,即可以分别沿三个坐标轴作平移和旋转动作,四个 控制自由度 ,即四个电机的转速。飞行器由四个可以独立控制转速的外转子直流无刷电机驱动的螺旋桨提供全部动力,依据力的合成与分解及空气转动扭矩的反向性,通过各种不同的改变转速的方式,进行各种不同的飞行动作。
四旋翼飞行器从结构上来分类,主要可以分为 X模型 、 十模型 与 H模型(如图1所示),目前来说,最主流的是X模型,但是无论是哪一种模型,其基本的飞行原理是大同小异的。
从上图中可以发现, 相邻两个旋翼的转动方向是相反的 ,也就是说,对角线上两个电机的转动方向相同,这是因为,由于空气转动扭矩的反向性,旋翼在旋转时会产生反扭距,例如,顺时针方向转动的螺旋桨在转动时,空气会产生使得四轴逆时针方向转动的反向扭矩,而当M1与M4同方向、M2与M3同方向时,反向扭矩能够相互抵消,使得飞行器在偏航方向能够保持平衡,不至于出现自旋转。与传统的单旋翼飞行器,特别是直升机相比,省去了用尾桨(又称抗扭螺旋桨)来平衡反扭距,使得四旋翼飞行器的能量利用率更高。
另外,由于相邻两个旋翼的转动方向相反,为保证他们产生的升力皆向上,M1、M4电机使用 “正桨” ,即顺时针方向转动产生上升力的桨,M2、M3电机使用 “反桨” ,即逆时针方向转动产生上升力的桨。
图2与图3以“X模型”为例,对飞行器结构进行了简单描述。
¶2. 基本飞行动作
四旋翼飞行器可以分别沿着机体的 X、Y、Z 三个轴进行旋转或者平移运动,因此在每个轴向上有两个自由度,四旋翼飞行器有六种基本飞行动作:
- 垂直(升降)运动
- 俯仰运动
- 横滚(滚转)运动
- 偏航(自旋)运动
- 前后运动
- 侧向运动
下面以十字模式说明六种运动的原理:
¶2.1 垂直运动
在图 a 中,因有两对电机转向相反,可以平衡其对机身的反扭矩,当同时增加四个电机的输出功率,旋翼转速增加使得总的拉力增大,当总拉力足以克服整机的重量时,四旋翼飞行器便离地垂直上升;
反之,同时减小四个电机的输出功率,四旋翼飞行器则垂直下降,直至平衡落地,实现了沿 z 轴的垂直运动;
当外界扰动量为零时,在旋翼产生的升力等于飞行器的自重时,飞行器便保持悬停状态;
保证四个旋翼转速同步增加或减小是垂直运动的关键;
¶2.2 俯仰运动
在图 b 中,电机1的转速上升,电机3的转速下降,电机2、电机4的转速保持不变;
为了不因为旋翼转速的改变引起四旋翼飞行器整体扭矩及总拉力改变,旋翼1 与 旋翼3 转速该变量的大小应相等;
由于 旋翼1 的升力上升,旋翼3 的升力下降,产生的不平衡力矩使机身绕 y 轴旋转(方向如图所示),同理,当 电机1 的转速下降,电机3 的转速上升,机身便绕 y 轴向另一个方向旋转,实现飞行器的俯仰运动;
¶2.3 横滚运动
与图 b 的原理相同,在图 c 中,改变 电机2 和 电机4 的转速,保持 电机1 和 电机3 的转速不变,则可使机身绕 x 轴旋转(正向和反向),实现飞行器的横滚(滚转)运动;
¶2.4 偏航运动
四旋翼飞行器偏航运动可以借助旋翼产生的反扭矩来实现;
旋翼转动过程中由于空气阻力作用会形成与转动方向相反的反扭矩,为了克服反扭矩影响,可使四个旋翼中的两个正转,两个反转,且对角线上的来年各个旋翼转动方向相同;
反扭矩的大小与旋翼转速有关,当四个电机转速相同时,四个旋翼产生的反扭矩相互平衡,四旋翼飞行器不发生转动;
当四个电机转速不完全相同时,不平衡的反扭矩会引起四旋翼飞行器转动;
在图 d 中,当 电机1 和 电机3 的转速上升,电机2 和 电机4 的转速下降时,旋翼1 和 旋翼3 对机身的反扭矩大于 旋翼2 和 旋翼4 对机身的反扭矩,机身便在富余反扭矩的作用下绕z轴转动,实现飞行器的偏航运动,转向与 电机1、电机3 的转向相反;
因为电机的总升力不变,飞机不会发生垂直运动;
¶2.5 前后运动
要想实现飞行器在水平面内前后、左右的运动,必须在水平面内对飞行器施加一定的力;
在图 e 中,增加 电机3 转速,使拉力增大,相应减小 电机1 转速,使拉力减小,同时保持其它两个电机转速不变,反扭矩仍然要保持平衡;
按图 b 的理论,飞行器首先发生一定程度的倾斜,从而使旋翼拉力产生水平分量,因此可以实现飞行器的前飞运动,向后飞行与向前飞行正好相反;
当然在图 b 图 c 中,飞行器在产生俯仰、翻滚运动的同时也会产生沿 x、y 轴的水平运动;
¶2.6 侧向运动
在图 f 中,由于结构对称,所以侧向飞行的工作原理与前后运动完全一样;
¶3. 飞行姿态与电机转速关系
由于主流的设计思想是将四旋翼飞行器设计为X模型,这里给出X模型的飞行姿态与电机转速关系,原理与十模型基本一致。
不妨设悬停状态下4个电机的转速为M1、M2、M3、M4:
| 动作 | 电机1 | 电机2 | 电机3 | 电机4 | |
| 悬停 | / | M1 | M2 | M3 | M4 |
| / | |||||
| 垂直 | 上升 | M1+ | M2+ | M3+ | M4+ |
| 下降 | M1- | M2- | M3- | M4- | |
| 横滚 | 左移 | M1- | M2+ | M3- | M4+ |
| 右移 | M1+ | M2- | M3+ | M4- | |
| 俯仰 | 前移 | M1- | M2- | M3+ | M4+ |
| 后移 | M1+ | M2+ | M3- | M4- | |
| 偏航 | 顺时针 | M1- | M2+ | M3+ | M4- |
| 逆时针 | M1+ | M2- | M3- | M4+ | |
¶四、姿态解算分析
¶1. 概述
四旋翼飞行器具有6个自由度,通过 IMU 惯性测量单元 实时测量飞行器三个轴向的旋转角速度和加速度,进行数据融合与姿态解算,从而控制飞行器的4个输入控制量,以达到飞行器平衡飞行的目的。
其简易控制逻辑如图11所示,其中 GYRO 指 陀螺仪(Gyroscope) , ACC 指 加速度计(Accelerometer) , PWM 指 脉冲宽度调制(Pulse width modulation) , Remote 指 远端 。
姿态解算是 捷联式惯性导航系统(SINS) 的关键技术,通过位姿矩阵可以得到载体的姿态和导航参数计算需要的数据,是捷联式惯导算法中的重要工作。载体的姿态和航向体现了载体坐标系和导航坐标系之间的方位关系,确定两个坐标系之间的方位关系需要借助矩阵法和力学中的刚体定点运动的位移定理,通过矩阵法推导方向余弦表,而刚体定点运动的位移定理表明,定点运动刚体的任何有限位移都可以绕过定点的某一轴经过一次转动来实现。那么,一个动坐标系相对参考坐标系的方位可以完全由动坐标系一次让三个不同的轴转动的三个角度,即一组欧拉角来确定。
目前,描述动坐标相对参考坐标系方位关系的方法可以简单地将其分为三类,即三参数法,四参数法和九参数法,三参数法也称 欧拉角法 ,四参数法通常指 四元数法 ,九参数法称为 方向余弦法 。
欧拉角法推导出的微分方程式皆含有三角函数运算,计算速度慢,方程出现“奇点”,且实时计算困难,故难以广泛用于工程实践;方向余弦法避免了奇点现象,但方程的计算量大,工作效率低;相比较而言,四元数法更能够合理地描述载体的刚体空间运动。
¶2. 姿态模块
姿态模块可以使用 Invensense 公司的消费级陀螺仪传感器,如六轴系列的 MPU6050 、九轴系列的 MPU9250 等,可输出六轴数据的传感器模块包括基础的三轴(X, Y, Z)角速度数据,三轴加速度数据,而九轴系列传感器还会输出三轴地磁数据,如果在加上气压计芯片获取高度就会构成十轴传感器模块。
有了姿态模块输出角速度、加速度、地磁数据后,就能通过算法计算出四轴相对于地心坐标系偏差的角度,以及此时偏差的速度大小(角速度)。对于姿态计算可以使用 AHRS(航姿参考系统) 和 IMU(惯性测量单元) 算法。 AHRS 由加速度计、地磁计和陀螺仪构成,是一种相对广泛使用的算法。其优点是使用多组数据进行融合,保障了数据的准确性;其缺点是太过于依赖地磁数据进行融合,磁场传感器一旦受到干扰,数据融合就可能出错,造成严重后果。IMU 则放弃了地磁数据,单纯地用角速度计算出角度。当四轴处于惯性参考系中飞行效果与 AHRS 比较相差甚微,而当四轴突然加速或减速时,机体处于非惯性参考系下,加速计数据短暂失真,表现在四轴上会发生振荡现象。
¶3. IMU惯性导航姿态算法
¶3.1 算法分析
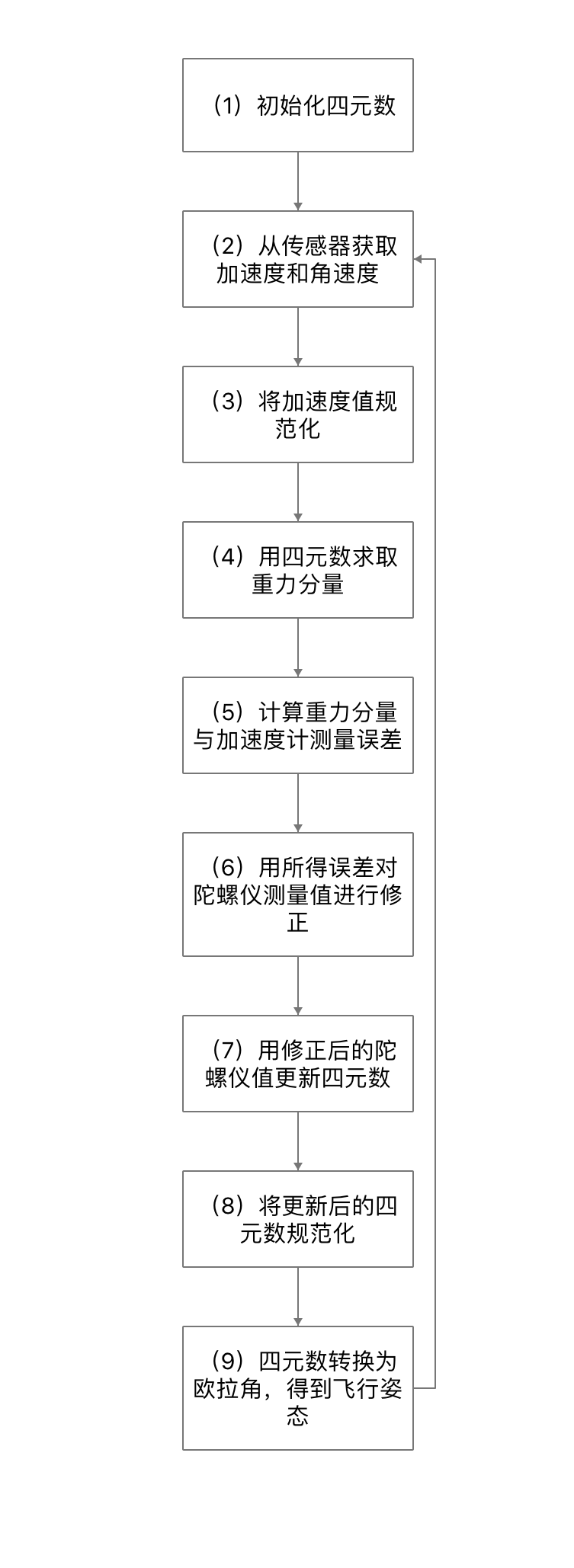
IMU惯性导航姿态算法,即利用四元数法进行姿态解算,其算法流程图如图12所示。
从流程图中可以看出,其主要思想还是利用加速度计对陀螺仪进行修正,其修正的快慢程度由参数进行控制,由于使用该方法步骤较为繁琐,涉及中间变量转换较多,且计算量较大,占用内存也较大,使用起来很不方便。为解决该问题,运动控制传感器(例如 MPU6050 )在内部提供了 DMP 四元数解算功能,可以直接输出四元数数据,从而省略了繁琐的计算步骤,给设计带来了极大便利,大大简化了四轴飞行器的代码设计量。
DMP(数字运动处理器) ,是 MPU 内部集成的处理单元,也就是说,MPU6050,或者MPU9250,并不单单是传感器,其内部还包含了可以独立完成姿态解算算法的处理单元。因其使用的是 Invensense 公司官方提供的姿态解算算法,与入门级的开发者相比有着较高的可靠性,且能够将微处理器从算法处理的压力中解放出来,只需要等待 DMP 解算完成后产生外部中断,在中断里读取姿态解算的结果,于是,在实际设计中,一般使用 DMP 来实现传感器融合算法,这里为了学习了解算法背后的飞行控制原理,对用四元数法进行姿态解算的算法进行深入分析。
¶3.2 坐标系统
为获取四旋翼飞行器控制系统的数学模型,必须先建立两个基本坐标系,即“地理”坐标系(惯性坐标系)和“载体”坐标系(机体坐标系)。“地理”坐标系指的就是地球上的 “东北天(ENU)”坐标系 ,而“载体”坐标系指的就是四轴自己的坐标系。
¶3.3 欧拉角与方向余弦矩阵
首先给出刚体定点运动的欧拉定理,又称刚体欧拉转动定理、欧拉旋转定理。
刚体定点运动的欧拉定理:
可以推知,空间中坐标系的任意旋转,等效于依次绕三个坐标系定轴的旋转,那么,一个动坐标系相对参考坐标系的方位可以完全由动坐标系一次让三个不同的轴转动的三个角度来确定。在四旋翼飞行器的控制系统中,动坐标系即指机体坐标系,而参考坐标系即为地球上的“东北天(ENU)”坐标系。
然后给出欧拉角的定义:
欧拉角:
刚体定点运动的自由度为3,如何选择3个变量,使它们既能简单、明确、单值地确定刚体位置,又能独立变化,这对简化定点运动的描述是非常重要的,刚体力学的奠基者欧拉(Leonhard Euler,1707一1783)成功地、巧妙地解决了这个问题,他选择3个角度,即著名的 欧拉角(Euler angles) 作为描述刚体定点运动的变量,具体选择方法如下:以固定点为原点建立静正坐标系 $o-\xi\eta\zeta$ ,再以固定点为原点建立与刚体固连的动坐标系 $o-xyz$ ,如下图所示:
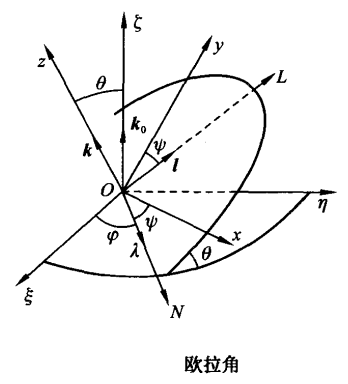
确定刚体位置等价于确定动坐标的位置,这里用两个角度确定 $z$ 轴的位置,一个是 $z$ 轴对 $\zeta$ 轴的倾角 $\theta$ 角,另一个是用来确定 $z$ 轴的方位,它是 $o-xy$ 面与平均赤道面 $o-\xi\eta$ 面的交线 $ON$ 与 $\xi$ 轴的夹角,交线 $ON$ 称为节线;这两个角确定后, $z$ 轴的位置就确定了,但动坐标系还可以绕 $z$ 轴转动,若动坐标的 $x$ 轴与节线的夹角 $\psi$ 确定了,则动坐标的位置完全确定,这样选取的3个角 $\theta$ , $\phi$ , $\psi$ 称为 欧拉角 。
它们的量度方向如图所示,它们的变化范围分别为:$0\le\theta\le\pi,0\le\phi\le2\pi,0\le\psi\le2\pi$ 。
为了表示动坐标系与参考坐标系的关系,引入 方向余弦 ,在研究两坐标系之间的运动特性时,方向余弦用矩阵的形式表示,称 方向余弦矩阵 ,也称为旋转矩阵、姿态矩阵,其元素是两组坐标系单位矢量之间夹角的正余弦值。
方向余弦与方向余弦矩阵:
方向余弦:
在解析几何里,一个向量的三个方向余弦分别是这向量与三个坐标轴之间的角度的余弦。两个向量之间的方向余弦指的是这两个向量之间的角度的余弦。
方向余弦矩阵:
方向余弦矩阵是由两组不同的标准正交基的基底向量之间的方向余弦所形成的矩阵。方向余弦矩阵可以用来表达一组标准正交基与另一组标准正交基之间的关系,也可以用来表达一个向量对于另一组标准正交基的方向余弦。
方向余弦方法可以用来设定附体参考系B的取向,即刚体的取向。假设沿着参考系 $S$ 的坐标轴的三个单位向量分别为 $\widehat{\boldsymbol x}_1,\widehat{\boldsymbol x}_2,\widehat{\boldsymbol x}_3$ ,沿着参考系 $B$ 的坐标轴的三个单位向量分别为 $\widehat{\boldsymbol e}_1,\widehat{\boldsymbol e}_2,\widehat{\boldsymbol e}_3$ 。定义 $\widehat{\boldsymbol e}_i$ 与 $\widehat{\boldsymbol x}_j$ 之间的方向余弦 ${a} _{ij}$ 为:
$$a_{ij}\overset{\underset{\mathrm{def}}{}}{=}cos({\theta}_{ij})=\widehat{\boldsymbol e}_i\cdot\widehat{\boldsymbol x}_j;$$
其中 ${\theta} _{ij}$ 是 $\widehat{\boldsymbol e}_i$ 与 $\widehat{\boldsymbol x}_j$ 之间的夹角。
$\widehat{\boldsymbol e}_1,\widehat{\boldsymbol e}_2,\widehat{\boldsymbol e}_3$ 与 $\widehat{\boldsymbol x}_1,\widehat{\boldsymbol x}_2,\widehat{\boldsymbol x}_3$ 之间的关系分别为: $$\widehat{\boldsymbol e}_1=cos({\theta}_{11})\cdot\widehat{\boldsymbol x}_1+cos({\theta}_{12})\cdot\widehat{\boldsymbol x}_2+cos({\theta}_{13})\cdot\widehat{\boldsymbol x}_3=a_{11}\widehat{\boldsymbol x}_1+a_{12}\widehat{\boldsymbol x}_2+a_{13}\widehat{\boldsymbol x}_3$$ $$\widehat{\boldsymbol e}_2=cos({\theta}_{21})\cdot\widehat{\boldsymbol x}_1+cos({\theta}_{22})\cdot\widehat{\boldsymbol x}_2+cos({\theta}_{23})\cdot\widehat{\boldsymbol x}_3=a_{21}\widehat{\boldsymbol x}_1+a_{22}\widehat{\boldsymbol x}_2+a_{23}\widehat{\boldsymbol x}_3$$ $$\widehat{\boldsymbol e}_3=cos({\theta}_{31})\cdot\widehat{\boldsymbol x}_1+cos({\theta}_{32})\cdot\widehat{\boldsymbol x}_2+cos({\theta}_{33})\cdot\widehat{\boldsymbol x}_3=a_{31}\widehat{\boldsymbol x}_1+a_{32}\widehat{\boldsymbol x}_2+a_{33}\widehat{\boldsymbol x}_3$$两个参考系的坐标轴所形成的矩阵称为方向余弦矩阵 $A$ :
$$A=\begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{bmatrix}$$采用爱因斯坦求和约定,由于 $\widehat{\boldsymbol e}_i=\sum_{}a_{ij}\cdot\widehat{\boldsymbol x}_j$ ,给定方向余弦矩阵 $A$ ,则可设定附体参考系 $B$ 的取向,也就是刚体的取向。
给定位置向量:
$$\boldsymbol r=x_1\widehat{\boldsymbol x}_1+x_2\widehat{\boldsymbol x}_2+x_3\widehat{\boldsymbol x}_3=e_1\widehat{\boldsymbol e}_1+e_2\widehat{\boldsymbol e}_2+e_3\widehat{\boldsymbol e}_3$$则 $\boldsymbol r$ 与 $\widehat{\boldsymbol e}_i$ 的内积为:
$$\boldsymbol r\cdot\widehat{\boldsymbol e}_i=e_i=a_{i1}x_1+a_{i2}x_2+a_{i3}x_3=a_{ij}x_j$$方向余弦矩阵 $A$ 可以将从空间参考系 $S$ 观测的位置坐标,变换为从附体参考系 $B$ 观测的位置坐标,因此又称为 变换矩阵 。
变换矩阵 $A$ 是一种正交矩阵,满足正交条件:
$$a_{ij}a_{jk}={\delta}_{ik}$$
其中 ${\delta}_{ik}$ 为 克罗内克函数 ,满足 ${\delta}_{ik}\begin{cases} 1\ \ \ \ (i=k) \\ 0\ \ \ \ (i \neq k) \end{cases}$ 。
变换矩阵可以视为旋转矩阵。例如将附体参考系 $B$ 或刚体旋转,从 $\widehat{\boldsymbol e}_1,\widehat{\boldsymbol e}_2,\widehat{\boldsymbol e}_3$ 旋转 $\theta$ 角弧成为 $\widehat{\boldsymbol e}‘_1,\widehat{\boldsymbol e}’_2,\widehat{\boldsymbol e}‘_3$ ;其中, $\widehat{\boldsymbol e}_3=\widehat{\boldsymbol e}’_3$ 。对于这个旋转,旋转矩阵 $A$ 为:
$$A=\begin{bmatrix} cos\theta & sin\theta & 0 \\ -sin\theta & cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix}$$有了以上数学物理工具的支持,可以开始对四旋翼飞行器的空间姿态进行描述。
¶3.4 空间姿态常规描述
分别定义欧拉角:
$\psi$ 为飞行器的航角, $\theta$ 为飞行器的仰角, $\phi$为飞行器的滚角。
那么需求得用三个欧拉角 $(\phi,\theta,\psi)$ 表示的机体坐标系与参考坐标系之间的方向余弦矩阵:
将机体坐标系 $b$ 的转动分解为分别绕参考坐标系 $n$ 的 $X,Y,Z$ 轴的简单转动,如图14所示:(注意笛卡尔坐标系左手系与右手系的区别,此处使用右手系)
分别求解三次简单转动的方向余弦矩阵:
这里以绕 $Z$ 轴的简单转动为例,说明求解过程,其余直接给出其方向余弦矩阵。
如图15所示,点 $v$ 绕原点旋转 $\alpha$ 角,得到点 $v’$,假设 $v$ 点的坐标为 $(x,y)$ ,那么可以推导得到 $v’$ 点的坐标 $(x’,y’)$ (设原点到点 $v$ 的距离为 $r$ ,原点到点 $v$ 的向量与 $X$ 轴的夹角为 $\beta$):
$$x=rcos\beta$$
$$y=rsin\beta$$
$$x’=rcos(\alpha+\beta)$$
$$y’=rsin(\alpha+\beta)$$
通过三角函数展开得到:
$$x’=rcos\alpha cos\beta - rsin\alpha sin\beta$$
$$y’=rsin\alpha cos\beta + rcos\alpha sin\beta$$
将 $x,y$ 代入得:
$$x’=xcos\alpha-ysin\alpha$$
$$y’=xsin\alpha+ycos\alpha$$
由于 $Z$ 为旋转轴,所以 $z$ 坐标保持不变:
$$z’=z$$
将方程组写成矩阵形式:
$$\begin{bmatrix}x' \\y' \\z' \end{bmatrix}=\begin{bmatrix}cos\alpha & -sin\alpha & 0 \\sin\alpha & cos\alpha & 0 \\0 & 0 & 1\end{bmatrix}\begin{bmatrix}x \\y \\z \end{bmatrix}$$将 $\alpha$ 角替换为飞行器的航角 $\psi$:
$$\begin{bmatrix}x' \\y' \\z' \end{bmatrix}=\begin{bmatrix}cos\psi & -sin\psi & 0 \\sin\psi & cos\psi & 0 \\0 & 0 & 1\end{bmatrix}\begin{bmatrix}x \\y \\z \end{bmatrix}$$即有:
$$C^{b3}_{n}=\begin{bmatrix}cos\psi & -sin\psi & 0 \\sin\psi & cos\psi & 0 \\0 & 0 & 1\end{bmatrix}$$同理可得:
绕 $Y$ 轴转动:
$$C^{b2}_{n}=\begin{bmatrix}cos\theta & 0 & -sin\theta \\0 & 1 & 0 \\sin\theta & 0 & cos\theta\end{bmatrix}$$绕 $X$ 轴转动:
$$C^{b1}_{n}=\begin{bmatrix}1 & 0 & 0 \\0 & cos\phi & sin\phi \\0 & -sin\phi & cos\phi\end{bmatrix}$$则用三个欧拉角 $(\phi,\theta,\psi)$ 表示的机体坐标系与参考坐标系之间的方向余弦矩阵可求得为:
$$C^b_n=C^{b1}_{n}C^{b2}_{n}C^{b3}_{n}=\begin{bmatrix}1 & 0 & 0 \\0 & cos\phi & sin\phi \\0 & -sin\phi & cos\phi\end{bmatrix}\begin{bmatrix}cos\theta & 0 & -sin\theta \\0 & 1 & 0 \\sin\theta & 0 & cos\theta\end{bmatrix}\begin{bmatrix}cos\psi & -sin\psi & 0 \\sin\psi & cos\psi & 0 \\0 & 0 & 1\end{bmatrix}$$$$C^b_n=\begin{bmatrix}cos\theta cos\psi+sin\theta sin\psi sin\phi & sin\theta cos\psi sin\phi - cos\theta sin\psi & -sin\theta cos\phi \\sin\psi cos\phi & cos\psi cos\phi & sin\phi \\sin\theta cos\psi - cos\theta sin\psi sin\phi & -cos\theta cos\psi sin\phi - sin\theta sin\psi & cos\theta cos\phi\end{bmatrix}$$
如何应用该结论呢?
记:
$$C^n_b=\begin{bmatrix}T_{11} & T_{12} & T_{13} \\T_{21} & T_{22} & T_{23} \\T_{31} & T_{32} & T_{33}\end{bmatrix}$$则由于矩阵正交,有:
$$C^n_b=(C^b_n)^{T}=\begin{bmatrix}T_{11} & T_{21} & T_{31} \\T_{12} & T_{22} & T_{32} \\T_{13} & T_{23} & T_{33}\end{bmatrix}$$根据矩阵可以反解出三个轴的角度——欧拉角:
$$\begin{cases} \phi=arcsin(T_{32}) \\\\ \theta=arctan(-{\dfrac {T_{31}}{T_{33}}}) \\\\ \psi=arctan(\dfrac {T_{12}}{T_{22}}) \end{cases}$$ 但该结论还不能够应用到四旋翼姿态解算中:
(1)函数与自变量量相同;
(2)含有大量三角运算,加重了运算负担,拖慢了运算效率。
在此思路上,希望能够换一种变量来表示该矩阵,保证方程可解的基础上还能提高运算效率。
于是引入四元数与罗德里格旋转公式。
¶3.5 四元数
四元数(Quaternions) 是由爱尔兰数学家哈密顿(William Rowan Hamilton,1805-1865)在1843年发明的数学概念。它是简单的超复数。 复数是由实数加上虚数单位 $i$ 组成,其中 $i^2=-1$ 。 相似地,四元数都是由实数加上三个虚数单位 $i、j、k$ 组成,而且它们有如下的关系: $i^2 = j^2 = k^2 = -1, i^0 = j^0 = k^0 = 1$ , 每个四元数都是 $1、i、j$ 和 $k$ 的线性组合,即是四元数一般可表示为 $a + bi+ cj + dk$ ,其中 $a、b、c 、d$ 是实数。
明确地说,四元数是复数的不可交换延伸。如把四元数的集合考虑成多维实数空间的话,四元数就代表着一个四维空间,相对于复数为二维空间。
四元数有如下的表达形式:
$$Q=q_0 + q_1 \dot i + q_2 \dot j+q_3 \dot k$$
$$Q=cos{\dfrac \theta 2}+\vec{\lambda}sin{\dfrac \theta 2}$$
$$Q=\begin{bmatrix}q_0 \\q_1 \\q_2 \\q_3 \end{bmatrix}$$¶3.6 罗德里格旋转公式
为了让空间中旋转的坐标变换过程能够与四元数之间建立关系,可以以某向量为研究对象引入更广义的空间旋转过程的计算公式——罗德里格旋转公式。
罗德里格旋转公式(Rodrigues’ rotation formula) 是计算三维空间中,一个向量绕旋转轴旋转给定角度以后得到的新向量的计算公式。这个公式使用原向量,旋转轴及它们叉积作为标架表示出旋转以后的向量。可以改写为矩阵形式,被广泛应用于空间解析几何和计算机图形学领域,成为刚体运动的基本计算公式。
四元数可以很方便地表示旋转变换。但在很多场合中,使用矩阵形式和向量形式表达旋转更有利于推导。向量旋转公式最早由法国数学家本杰明·奥伦德·罗德里格(Benjamin Olinde Rodrigues(1795–1851))导出,后来被应用在很多领域。
设v是一个三维空间向量,$\boldsymbol k$ 是旋转轴的单位向量,则 $\boldsymbol v$ 在右手螺旋定则意义下绕旋转轴 $\boldsymbol k$ 旋转角度 $\theta$ 得到的向量可以由三个不共面的向量 $\boldsymbol v,\boldsymbol k$ 和 $\boldsymbol k \times \boldsymbol v$ 构成的标架表示:
$$\boldsymbol v_{rot}=cos\theta \cdot \boldsymbol v+(1-cos\theta)(\boldsymbol v \cdot \boldsymbol k)\boldsymbol k+sin\theta \cdot \boldsymbol k \times \boldsymbol v$$
根据此公式推导可得以下结论:
$$\overrightarrow{D B}^{R}=U \cdot \overrightarrow{D B}^{b}$$
$U$ 为刚体旋转过程中 $b$ 系到 $R$ 系的坐标变换矩阵:
$$U=C_b^R=I+2Jcos{\dfrac \theta 2}+2K$$
其中:
$I$ 为三阶单位矩阵:
$$I=\begin{bmatrix}1 & 0 & 0 \\0 & 1 & 0 \\0 & 0 & 1 \end{bmatrix}$$$$J=\begin{bmatrix}0 & -nsin{\dfrac \theta 2} & msin{\dfrac \theta 2} \\\\nsin{\dfrac \theta 2} & 0 & -lsin{\dfrac \theta 2} \\\\-msin{\dfrac \theta 2} & lsin{\dfrac \theta 2} & 0 \end{bmatrix}$$
$$K= \begin{bmatrix}-(m^2+n^2)sin^2{\dfrac \theta 2} & lmsin^2{\dfrac \theta 2} & nlsin^2{\dfrac \theta 2} \\\\lmsin^2{\dfrac \theta 2} & -(l^2+n^2)sin^2{\dfrac \theta 2} & mnsin^2{\dfrac \theta 2} \\\\nlsin^2{\dfrac \theta 2} & mnsin^2{\dfrac \theta 2} & -(m^2+l^2)sin^2{\dfrac \theta 2} \end{bmatrix}$$
在 $K$ 中, $l、m、n$ 分别是向量 $\overrightarrow{D E}$ 在 $R$ 系的旋转瞬轴,结合四元数的三角表示式,令:
$$Q=cos{\dfrac \theta 2}+(l\boldsymbol i+m\boldsymbol j+n\boldsymbol k)sin{\dfrac \theta 2}$$
即有:
$$\begin{cases} q_0=cos{\dfrac \theta 2} \\\\ q_1=lsin{\dfrac \theta 2} \\\\ q_2=msin{\dfrac \theta 2} \\\\ q_3=nsin{\dfrac \theta 2} \end{cases}$$将 $q$ 代入 $U$,$U$ 等价于方向余弦矩阵:
$$C_b^R=\begin{bmatrix} q_0^2+q_1^2-q_2^2-q_3^2 & 2(q_1 q_2-q_0 q_3) & 2(q_1 q_3+q_0 q_2) \\ \\ 2(q_1 q_2+q_0 q_3) & q_0^2-q_1^2+q_2^2-q_3^2 & 2(q_3 q_2-q_0 q_1) \\ \\ 2(q_1 q_3-q_0 q_2) & 2(q_3 q_2+q_0 q_1) & q_0^2-q_1^2-q_2^2+q_3^2 \end{bmatrix}$$于是可以反解欧拉角:
$$\begin{cases} \phi=arcsin(T_{32})=arcsin(C_{23}) \\\\ \theta=arctan(-{\dfrac {T_{31}}{T_{33}}})=arctan(-{\dfrac {C_{13}}{C_{33}}}) \\\\ \psi=arctan(\dfrac {T_{12}}{T_{22}})=arctan(\dfrac {C_{21}}{C_{22}}) \end{cases}$$可得:
$$\begin{cases} \phi=arcsin[2(-q_0 q_1+q_2 q_3)] \\\\ \theta=-arctan({\dfrac{2(q_0 q_2+q_1 q_3)}{q_0^2-q_1^2-q_2^2+q_3^2}}) \\\\ \psi=arctan({\dfrac{2(q_1 q_2+q_0 q_3)}{q_0^2-q_1^2+q_2^2-q_3^2}}) \end{cases}$$那么现在问题就变成了如何求取四元数中的 $q_0、q_1、q_2、q_3$ 。
¶3.7 四元数的求解与一阶龙格-库塔法
到目前为止,飞行器姿态的改变已经转换成了对应四元数的改变,因此实时的姿态计算需要实时更新四元数。于是在此构建四元数关于时间的微分方程,来研究四元数的变化规律,又因为考虑到与四元数直接相关的变量是角度,因此,利用四元数的三角表示式来建立四元数微分方程,并求解该微分方程,即可成功解出四元数。
$$Q=cos{\dfrac \theta 2}+\vec{\lambda}sin{\dfrac \theta 2}$$
令该四元数对时间 $t$ 进行微分,可得微分方程为:
$$\dfrac{\mathrm{d}Q}{\mathrm{d}t}={\dfrac 1 2} \begin{bmatrix} 0 & -{\omega}_x & -{\omega}_y & -{\omega}_z \\ {\omega}_x & 0 & {\omega}_z & -{\omega}_y \\ {\omega}_y & -{\omega}_z & 0 & {\omega}_x \\ {\omega}_z & {\omega}_y & -{\omega}_x & 0 \end{bmatrix} \begin{bmatrix}q_0 \\q_1 \\q_2 \\q_3 \end{bmatrix}$$记为:
$$\dfrac{\mathrm{d}Q}{\mathrm{d}t}=\Phi \cdot Q$$
求解该微分方程即可得到当下的四元数。
为了在单片机中能够求解微分方程,引入一阶龙格-库塔法。
一阶龙格-库塔法(Runge-Kutta):
龙格-库塔(Runge-Kutta)方法是一种在工程上应用广泛的高精度单步算法,其中包括著名的欧拉法(Euler’s method),用于数值求解微分方程,该算法是构建在数学支持的基础之上的。
一阶龙格库塔法,即对应于“一阶精度欧拉公式”:
$$\begin{cases} y'=\dfrac{\mathrm{d}y}{\mathrm{d}x}=f(x,y) \\\\ y_{i+1}=y_i+h\cdot K_1 \\\\ K_1= f(x_i,y_i) \end{cases}$$其中 $h$ 为步长。
设有微分方程:
$$\dfrac{\mathrm{d}y}{\mathrm{d}x}=f(x,y)$$根据一阶龙格-库塔法可以得到求解 $y$ 的迭代公式:
$$y(\lambda + \Delta\lambda)=y(\lambda)+\Delta\lambda\cdot f(x(\lambda),y(\lambda))$$对应四元数微分方程:
$$Q(t + \Delta t)=Q(t)+\Delta t \cdot \Phi(t) \cdot Q(t)$$整理可得最终的计算结论:
$$\begin{bmatrix}q_0 \\q_1 \\q_2 \\q_3 \end{bmatrix}_{t+\Delta t}=\begin{bmatrix}q_0 \\q_1 \\q_2 \\q_3 \end{bmatrix}_t+{\dfrac 1 2} \cdot \Delta t \cdot \begin{bmatrix} -\omega_x \cdot q_1-\omega_y \cdot q_2-\omega_z \cdot q_3 \\ \omega_x \cdot q_0-\omega_y \cdot q_3+\omega_z \cdot q_2 \\ \omega_x \cdot q_3+\omega_y \cdot q_0-\omega_z \cdot q_1 \\ -\omega_x \cdot q_2+\omega_y \cdot q_1+\omega_z \cdot q_0 \end{bmatrix}$$对该结论利用C语言编程,即可实现对四元数的求解,而求解过程中需要用到三轴角速度数据,要想准确获取机体的实时姿态,则要求三轴角速度数据足够准确,可行的想法是,利用加速度计对陀螺仪的数据进行修正。
¶3.8 传感器数据融合——基于四元数的互补滤波法(向量外积补偿)
互补滤波法(Complementary Filter) 的思路是,加速度计由于其自身灵敏度较高,在振动较大的场合,加速度计的测量值容易混入振动等噪声,也就是说,加速度计在瞬时精度上容易受到外部干扰,而有很大误差,这种误差属于高频误差;陀螺仪的测量值是角速度,短时间内将角速度按时间积分得到的角度是比较准确的,但是此时得到的角度带有累积误差,这种误差属于低频误差。可以利用这两种传感器的特性来互补,得到正确的角度。
但是这里并不打算用常规的互补滤波算法来实现互补滤波,而是采用向量外积补偿的方法来实现。
在图20中,$a_x,a_y,a_z$ 为机体坐标参考系上加速度计测出来的重力加速度分量经过单位化后得到的单位重力加速度分量,相当于是实际重力加速度分量;$v_x,v_y,v_z$ 为用三轴陀螺仪角速度数据经过换算、积分后得到的单位重力加速度分量,相当于是理论重力加速度分量。若能够表示出两者之间的误差,就能够用这个误差去补偿陀螺仪输出的角速度,从而计算出更新的四元数。
这个误差属于向量之间的误差,可以用向量外积(即向量叉积)来表示。
这个向量叉积仍然是位于机体坐标系上的,而陀螺积分误差也在机体坐标系上,而且叉积的大小与陀螺积分误差呈正比,正好拿来补偿陀螺仪角速度数据。
¶3.9 构建PI(比例-积分)控制器
得到用向量外积表示的误差后,接下来需要构建PI(比例-积分)控制器来控制补偿值的大小与精度。(其中有关自动控制原理特性的分析,此处不再体现)
$$error\_GYRO=K_p\cdot error+K_I\cdot \int error$$积分项用来消除静态误差,比例项用来控制传感器的“可信度”,$K_p$ 越大,则更加信任加速度计,$K_p$ 越小,则更加信任陀螺仪。
把补偿量加到角速度上,即可得到可信度较高的陀螺仪数据,之后代入龙格库塔法即可得到当前的四元数。
$$value\_GYRO=value\_GYRO+error\_GYRO$$¶3.10 算法流程与总体代码分析
¶3.10.1 四元数法姿态解算流程
(1)初始化四元数:
设当前的坐标系为机体坐标系,则四元数列向量:
$$\boldsymbol q=\begin{bmatrix}q_0 & q_1 & q_2 & q_3 \end{bmatrix}^T= \begin{bmatrix}1 & 0 & 0 & 0 \end{bmatrix}^T$$(2)获取角速度、加速度:
读取三轴加速度计和三轴陀螺仪的信号,并经过IIR低通滤波器滤波滤除振动噪声,得到重力加速度分量和角速度分量 $acc_x,acc_y,acc_z$ 和角速度分量 $w_x,w_y,w_z$ 。
(3)将加速度计测量值 $acc_x,acc_y,acc_z$ 转化为三维的单位向量(归一化):
$$\begin{cases} a_x={\dfrac {acc_x}{\sqrt {acc_x^2+acc_y^2+acc_z^2}}} \\\\ a_y={\dfrac {acc_y}{\sqrt {acc_x^2+acc_y^2+acc_z^2}}} \\\\ a_z={\dfrac {acc_z}{\sqrt {acc_x^2+acc_y^2+acc_z^2}}} \end{cases}$$代码实现:
1 | norm = sqrt(ax * ax + ay * ay + az * az); |
(4)用四元数表示三轴的重力分量 $V_x,V_y,V_z$:
(对应着已求出的用四元数表示的方向余弦矩阵 $C_b^R$ 的第三行)
式中的 $V_x,V_y,V_z$ 即重力单位向量在机体坐标系中的分量。
代码实现:
1 | vx = 2 * (q1 * q3 - q0 * q2); |
(5)求四元数所求重力分量与加速度计测量值的误差值:
$$\begin{cases} e_x=a_y \times V_z - a_z \times V_y \\\\ e_y=a_z \times V_x - a_x \times V_z \\\\ e_z=a_x \times V_y - a_y \times V_x \end{cases}$$代码实现:
1 | ex = (ay * vz - az * vy); |
(6)利用所得的误差修正陀螺仪的测量值:
(式中参数 $k_i,k_p$ 用以控制加速度计修正陀螺仪误差的过程)
代码实现:
1 | exInt = exInt + ex * Ki; |
(7)利用修正后的陀螺仪值 ${\dot w}_x,{\dot w}_y,{\dot w}_z$ 更新四元数:
$$\begin{cases} q_0={\widehat q}_0+{\dfrac {\mathrm{d}t}{2}}(-q_1{\dot w}_x-q_2{\dot w}_y-q_3{\dot w}_z) \\\\ q_1={\widehat q}_1+{\dfrac {\mathrm{d}t}{2}}(q_0{\dot w}_x+q_2{\dot w}_z-q_3{\dot w}_y) \\\\ q_2={\widehat q}_2+{\dfrac {\mathrm{d}t}{2}}(q_0{\dot w}_y-q_1{\dot w}_z+q_3{\dot w}_x) \\\\ q_3={\widehat q}_3+{\dfrac {\mathrm{d}t}{2}}(q_0{\dot w}_z+q_1{\dot w}_y-q_2{\dot w}_x) \end{cases}$$代码实现:
1 | q0 = q0 + (-q1 * gx - q2 * gy - q3 * gz) * halfT; |
(8)将得到更新后的四元数规范化:
$$\begin{cases} q_0={\dfrac {\widehat q_0}{\sqrt {q_0^2+q_1^2+q_2^2+q_3^2}}} \\\\ q_1={\dfrac {\widehat q_1}{\sqrt {q_0^2+q_1^2+q_2^2+q_3^2}}} \\\\ q_2={\dfrac {\widehat q_2}{\sqrt {q_0^2+q_1^2+q_2^2+q_3^2}}} \\\\ q_3={\dfrac {\widehat q_3}{\sqrt {q_0^2+q_1^2+q_2^2+q_3^2}}} \end{cases}$$代码实现:
1 | norm = sqrt(q0 * q0 + q1 * q1 + q2 * q2 + q3 * q3); |
(9)得到新四元数后,即完成了一次四元数法姿态融合的运算,将新的四元数作为下一次四元数运算的初始四元数,再从步骤(1)开始下一次的四元数运算。为了直观表示飞行器的姿态,可将新四元数转化成为三个欧拉角:
$$\begin{cases} \phi=arcsin[2(-q_0 q_1+q_2 q_3)] \\\\ \theta=-arctan({\dfrac{2(q_0 q_2+q_1 q_3)}{q_0^2-q_1^2-q_2^2+q_3^2}}) \\\\ \psi=arctan({\dfrac{2(q_1 q_2+q_0 q_3)}{q_0^2-q_1^2+q_2^2-q_3^2}}) \end{cases}$$这里提供了两种代码进行参考:
1 | pitch = asin(2 * (q0 * q2 - q1 * q3)) * 57.2957795f; |
¶3.10.2 总体代码
1 | /**********/ |
¶五、总结
¶1. 全文总结
本文以四旋翼飞行器的飞行原理与姿态解算的分析为背景,目的是深入研究四旋翼飞行器的姿态解算算法,从而理解其软件设计的基本原理,并为动手设计一款四旋翼飞行器奠定基础。本文主要进行的研究工作与成果如下:
1)四旋翼飞行器的飞行原理。本文对四旋翼飞行器的基本飞行原理与基本结构进行了简要的描述,对飞行器能够做出的基本飞行动作的动力学原理进行了基本的分析,给出了飞行器飞行姿态与其电机转速的关系。
2)四旋翼飞行器的姿态解算算法。本文基于 Madgwick 的 IMUupdate 算法,对四旋翼飞行器的姿态解算算法从其数学原理以及其算法优化上进行了深入的分析,为今后飞行器姿态解算的软件设计提供了基础。
¶2. 个人总结
在本次科研选题训练过程中,我对该领域的知识进行了深入的认识与了解,加强了自身检索文献的能力,培养了自身撰写论文的能力,增强了小组合作探究的能力。总的来说,这是一次收获颇丰的体验。
¶参考资料
看了各种各样的资料,其中有的资料中还存在一些错误,我将其一并放在这里了,如果读者有兴趣阅读,一定要注意。
¶文献
[1] 王瑞,丁晓青 编著 . 四旋翼飞行器设计与实现 . 北京:清华大学出版社, 2018.
[2] 冯新宇,范红刚,辛亮 著 . 四旋翼无人飞行器设计 . 北京:清华大学出版社, 2017.
[3] 严恭敏,翁浚 编著 . 捷联惯导算法与组合导航原理讲义 . 西北工业大学, 2016.
[4] 喻金峰 . 四旋翼飞行器设计与实现[D] . 华南理工大学, 2018.
[5] 赵杰 . 基于模型的多旋翼飞行器飞控系统设计与实现[D] . 电子科技大学, 2019.
¶网页
常微分方程的解法 (三): 龙格—库塔(Runge—Kutta)方法 、线性多步法
¶视频
非常感谢b站up主Rick_Grimes对于姿态解算算法的总结,本文在分析姿态解算算法时是基于对其视频的思路与内容的概括与提炼。视频中同样也有一些错误,但不影响对于总体算法的理解。
视频链接:【教程】四旋翼飞行器姿态解算算法入门学习-Rick Grimes

