最短路算法笔记

Dijkstra
Floyd

¶Dijkstra

讨论带权有向图

路径上的第一个顶点——源点（Source）
最后一个顶点——终点（Destination）

从某个源点到其余各顶点的最短路径

Dijkstra 算法

单源最短路径算法

引进一个辅助向量 $D$

它的每个分量 $D[\ i \ ]$ 表示当前所找到的从始点 $v$ 到每个终点 $v_{i}$ 的最短路径的长度

初态：若从 $v$ 到 $v_{i}$ 有弧，则 $D[\ i \ ]$ 为弧上的权值，否则置 $D[\ i \ ]$ 为 $\infty$

从 $v$ 出发的长度最短的一条最短路径 $(v,v_{j})$ :

$D[\ j \ ] = Min\{\ D[\ i \ ] \ \big| \ v_{i} \in V \}$

按路径长度递增的次序来产生各最短路径

下一条长度次短的最短路径：

$D[\ j \ ] = Min\{\ D[\ i \ ] \ \big| \ v_{i} \in V - S\}$

步骤表达式

（1）$D[\ i \ ] = arcs[\ Locate Vex(G, v) \ ]\ [\ i \ ]\ \ \ \ v_{i} \in V$

（2）$D[\ i \ ] = Min\{\ D[\ i \ ] \ \big| \ v_{i} \in V - S\}\ \ \ \ S = S \bigcup \{j \}$

（3）若$ D[\ i \ ] + arcs[\ j \ ] [\ k \ ] < D[\ k \ ]\ ,\ D[\ k \ ] = D[\ i \ ] + arcs[\ j \ ] [\ k \ ]$

（4）重复(2)(3)共 $n - 1$ 次

算法示例

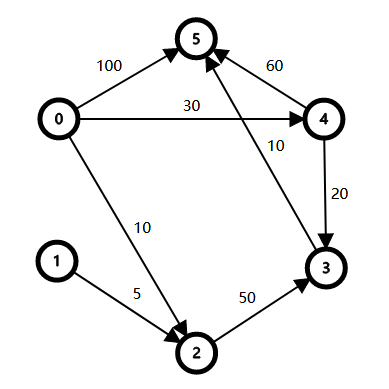
始点	终点	最短路径	路径长度
$v_0$	$v_1$	无
	$v_2$	$(v_0, v_2)$	$10$
	$v_3$	$(v_0, v_2, v_3)$	$60$
	$v_4$	$(v_0, v_4)$	$30$
	$v_5$	$(v_0, v_4, v_3, v_5)$	$60$

邻接矩阵

$\begin{pmatrix} \infty & \infty & 10 & \infty & 30 & 100 \\ \infty & \infty & 5 & \infty & \infty & \infty \\ \infty & \infty & \infty & 50 & \infty & \infty \\ \infty & \infty & \infty & \infty & \infty & 10 \\ \infty & \infty & \infty & 20 & \infty & 60 \\ \infty & \infty & \infty & \infty & \infty & \infty \end{pmatrix}$

（1）初始化$\ \ \ \ D[\ i \ ] = arcs[\ Locate Vex(G, v) \ ]\ [\ i \ ]\ \ \ \ v_{i} \in V$

$\ \ \ \ D[\ 0 \ ] = \infty\ \ \ \ D[\ 1 \ ] = \infty\ \ \ \ D[\ 2 \ ] = 10\ \ \ \ D[\ 3 \ ] = \infty\ \ \ \ D[\ 4 \ ] = 30\ \ \ \ D[\ 5 \ ] = 100$
$\ \ \ \ D[\ 0 \ ] = 0 \ \ \ \ S = \{\ 0 \ \}$ 第一个点，即始点

（2）$D[\ i \ ] = Min\{\ D[\ i \ ] \ \big| \ v_{i} \in V - S\}\ \ \ \ S = S \bigcup \{j \}$

$\ \ \ \ V - S = \{\ 1, 2, 3, 4, 5 \ \}$

找到与 $v_0$ 最近的点：$v_2\ \ \ \ min = 10\ \ \ \ D[\ 2 \ ] = 10\ \ \ \ S = \{\ 0,2 \ \}$

（3）若$ D[\ i \ ] + arcs[\ j \ ] [\ k \ ] < D[\ k \ ]\ ,\ D[\ k \ ] = D[\ i \ ] + arcs[\ j \ ] [\ k \ ]$

$\ \ \ \ 10(v_0 \rightarrow v_2) + \infty(v_2 \rightarrow v_1) > \infty(v_0 \rightarrow v_1)$ ，不满足， $D[\ 1 \ ] = \infty$
$\ \ \ \ 10(v_0 \rightarrow v_2) + 50(v_2 \rightarrow v_3) < \infty(v_0 \rightarrow v_3)$ ，满足， $D[\ 3 \ ] = 60$

后面皆不满足， $D[\ 4 \ ] = 30\ \ \ \ D[\ 5 \ ] = 100$

重复(2)(3)

（2’）$D[\ i \ ] = Min\{\ D[\ i \ ] \ \big| \ v_{i} \in V - S\}\ \ \ \ S = S \bigcup \{j \}$

$\ \ \ \ V - S = \{\ 1, 3, 4, 5 \ \}$

找到与 $v_0$ 最近的点：$v_4\ \ \ \ min = 30\ \ \ \ D[\ 4 \ ] = 30\ \ \ \ S = \{\ 0,2,4 \ \}$

（3’）若$ D[\ i \ ] + arcs[\ j \ ] [\ k \ ] < D[\ k \ ]\ ,\ D[\ k \ ] = D[\ i \ ] + arcs[\ j \ ] [\ k \ ]$

$\ \ \ \ 30(v_0 \rightarrow v_4) + \infty(v_4 \rightarrow v_1) > \infty(v_0 \rightarrow v_1)$ ，不满足， $D[\ 1 \ ] = \infty$
$\ \ \ \ 30(v_0 \rightarrow v_4) + 20(v_4 \rightarrow v_3) < 60(v_0 \rightarrow v_3)$ ，满足， $D[\ 3 \ ] = 50$
$\ \ \ \ 30(v_0 \rightarrow v_4) + 60(v_4 \rightarrow v_5) < 100(v_0 \rightarrow v_3)$ ，满足， $D[\ 3 \ ] = 90$

（2’’）$D[\ i \ ] = Min\{\ D[\ i \ ] \ \big| \ v_{i} \in V - S\}\ \ \ \ S = S \bigcup \{j \}$

$\ \ \ \ V - S = \{\ 1, 3, 5 \ \}$

找到与 $v_0$ 最近的点：$v_3\ \ \ \ min = 50\ \ \ \ D[\ 3 \ ] = 50\ \ \ \ S = \{\ 0,2,3,4 \ \}$

（3’’）若$ D[\ i \ ] + arcs[\ j \ ] [\ k \ ] < D[\ k \ ]\ ,\ D[\ k \ ] = D[\ i \ ] + arcs[\ j \ ] [\ k \ ]$

$\ \ \ \ 50(v_0 \rightarrow v_3) + \infty(v_3 \rightarrow v_1) > \infty(v_0 \rightarrow v_1)$ ，不满足， $D[\ 1 \ ] = \infty$
$\ \ \ \ 50(v_0 \rightarrow v_3) + 10(v_3 \rightarrow v_5) < 90(v_0 \rightarrow v_3)$ ，满足， $D[\ 5 \ ] = 60$

（2’’’）$D[\ i \ ] = Min\{\ D[\ i \ ] \ \big| \ v_{i} \in V - S\}\ \ \ \ S = S \bigcup \{j \}$

$\ \ \ \ V - S = \{\ 1, 5 \ \}$

找到与 $v_0$ 最近的点：$v_5\ \ \ \ min = 60\ \ \ \ D[\ 5 \ ] = 60\ \ \ \ S = \{\ 0,2,3,4,5 \ \}$

（3’’’）若$ D[\ i \ ] + arcs[\ j \ ] [\ k \ ] < D[\ k \ ]\ ,\ D[\ k \ ] = D[\ i \ ] + arcs[\ j \ ] [\ k \ ]$

$\ \ \ \ 10(v_0 \rightarrow v_5) + \infty(v_5 \rightarrow v_1) > \infty(v_0 \rightarrow v_1)$ ，不满足， $D[\ 1 \ ] = \infty$

（2’’’’）$D[\ i \ ] = Min\{\ D[\ i \ ] \ \big| \ v_{i} \in V - S\}\ \ \ \ S = S \bigcup \{j \}$

$\ \ \ \ V - S = \{\ 1 \ \}$

找到与 $v_0$ 最近的点：$v_1\ \ \ \ min = \infty\ \ \ \ D[\ 1 \ ] = \infty\ \ \ \ S = \{\ 0,1,2,3,4,5 \ \}$

（3’’’’）pass

(2)(3)共执行 $n-1 = 6-1 = 5$ 次，得到最短路径的带权长度

要想得到每条最短路径的具体路径，需持续更新 PathMatrix 二维数组

下面为 C 语言描述的 Dijkstra 算法

void shortestPath_DIJ(MGraph G, int v0, PathMatrix &P, ShortPathTable &D) {
    // 用 Dijkstra 算法求有向网 G 的 v0 顶点到其余顶点 v 的最短路径 P[v] 及其带权长度 D[v]
    // 若 p[v][w] 为 TRUE，则 w 是从 v0 到 v 当前求得最短路径上的顶点
    // final[v] 为 TRUE 当且仅当 v in S，即已经求得从 v0 到 v 的最短路径（final 为 S 集）
    for (v = 0; v < G.vexnum; ++v) {
        final[v] = FALSE; D[v] = G.arcs[v0][v];
        for (w = 0; w < G.vexnum; ++w)  P[v][w] = FALSE;
        if (D[v] < INFINITY) {P[v][v0] = TRUE; P[v][v] = TRUE;}
    } // for
    D[v0] = 0; final[v0] = TRUE;        // 初始化，v0 顶点入 S 集
    // 开始主循环，每次求得 v0 到某个 v 顶点的最短路径，并加 v 到 S 集
    for (i = 1; i < G.vexnum; ++i) {     // 其余 G.vexnum - 1 个顶点
        min = INFINITY;                 // 当前所知离 v0 顶点的最近距离
        for (w = 0; w < G.vexnum; ++w)
            if (!final[w])              // v0 in V-S 集
                if (D[w] < min) {v = w; min = D[w];}
                                        // 找到与 v0 最近的顶点（最小 D[w]）
        final[v] = TRUE;                // 找到后即加入 S 集
        for (w = 0; w < G.vexnum; ++v)  // 更新 D[w], P[w]
            if (!final[w] && (min + G.arcs[v][w] < D[w])) {
                D[w] = min + G.arcs[v][w];      // w in V-S 集
                P[w] = P[v]; P[w][w] = TRUE;    // P[w] = P[v] + P[w]
            } // if
    } // for
} // ShortestPath_DIJ

PathMatrix P 的更新

邻接矩阵

$P[\ 6 \ ] [\ 6 \ ]$

初始化 P 全为 FALSE

$D[\ 0 \ ] = \infty\ \ \ \ D[\ 1 \ ] = \infty\ \ \ \ D[\ 2 \ ] = 10\ \ \ \ D[\ 3 \ ] = \infty\ \ \ \ D[\ 4 \ ] = 30\ \ \ \ D[\ 5 \ ] = 100$
$if\ \ \ \ D[\ v \ ] < INFINITY \ \ \ \ P[\ v \ ] [\ v_0 \ ] = TRUE; \ \ \ \ P[\ v \ ] [\ v \ ] = TRUE;$
$\ \ \ \ P[\ 2 \ ] [\ 0 \ ] = TRUE; \ \ \ \ P[\ 2 \ ] [\ 2 \ ] = TRUE;$
$\ \ \ \ P[\ 4 \ ] [\ 0 \ ] = TRUE; \ \ \ \ P[\ 4 \ ] [\ 4 \ ] = TRUE;$
$\ \ \ \ P[\ 5 \ ] [\ 0 \ ] = TRUE; \ \ \ \ P[\ 5 \ ] [\ 5 \ ] = TRUE;$

$\begin{pmatrix} & & & & & \\ & & & & & \\ T & & T & & & \\ & & & & & \\ T & & & & T & \\ T & & & & & T \end{pmatrix}$

$P[\ w \ ] = P[\ v \ ]$

$P[w][w] = TRUE$

即 $P[\ w \ ] = P[\ v \ ] + P[\ w \ ]$

$10(v_0 \rightarrow v_2) + 50(v_2 \rightarrow v_3) < \infty(v_0 \rightarrow v_3)$ ，满足， $D[\ 3 \ ] = 60$
$D[\ 0 \ ] = 0\ \ \ \ D[\ 1 \ ] = \infty\ \ \ \ D[\ 2 \ ] = 10\ \ \ \ D[\ 3 \ ] = 60\ \ \ \ D[\ 4 \ ] = 30\ \ \ \ D[\ 5 \ ] = 100$

$\begin{pmatrix} & & & & & \\ & & & & & \\ T & & T & & & \\ T & & T & T & & \\ T & & & & T & \\ T & & & & & T \end{pmatrix}$

$30(v_0 \rightarrow v_4) + 20(v_4 \rightarrow v_3) < 60(v_0 \rightarrow v_3)$ ，满足， $D[\ 3 \ ] = 50$
$30(v_0 \rightarrow v_4) + 60(v_4 \rightarrow v_5) < 100(v_0 \rightarrow v_3)$ ，满足， $D[\ 3 \ ] = 90$
$D[\ 0 \ ] = 0\ \ \ \ D[\ 1 \ ] = \infty\ \ \ \ D[\ 2 \ ] = 10\ \ \ \ D[\ 3 \ ] = 50\ \ \ \ D[\ 4 \ ] = 30\ \ \ \ D[\ 5 \ ] = 90$

$\begin{pmatrix} & & & & & \\ & & & & & \\ T & & T & & & \\ T & & & T & T & \\ T & & & & T & \\ T & & & & T & T \end{pmatrix}$

$50(v_0 \rightarrow v_3) + 10(v_3 \rightarrow v_5) < 90(v_0 \rightarrow v_3)$ ，满足， $D[\ 5 \ ] = 60$
$D[\ 0 \ ] = 0\ \ \ \ D[\ 1 \ ] = \infty\ \ \ \ D[\ 2 \ ] = 10\ \ \ \ D[\ 3 \ ] = 50\ \ \ \ D[\ 4 \ ] = 30\ \ \ \ D[\ 5 \ ] = 60$

$\begin{pmatrix} & & & & & \\ & & & & & \\ T & & T & & & \\ T & & & T & T & \\ T & & & & T & \\ T & & & T & T & T \end{pmatrix}$

最终结果：

$D[\ 0 \ ] = 0\ \ \ \ D[\ 1 \ ] = \infty\ \ \ \ D[\ 2 \ ] = 10\ \ \ \ D[\ 3 \ ] = 50\ \ \ \ D[\ 4 \ ] = 30\ \ \ \ D[\ 5 \ ] = 60$

改进 $P$

无须二维数组，可以记录前驱

只须建立一个前驱顶点数组

$prev[\ i \ ]$ 的值为顶点 $v_s$ 到 $v_i$ 的最短路径所经历的全部结点中的 $v_i$ 的前驱

初始化时，$prev[\ i \ ] = 0 \ \ \ \ (i = 0; i < G.vexnum; i++)$

更新 D 数组时，更新 prev 数组，$prev[\ w \ ] = v$

	i	0	1	2	3	4	5
初始	prev[i]	0	0	0	0	0	0
	prev[i]				2			prev[3] = 2
	prev[i]				4		4	prev[1] = 4; prev[5] = 4
	prev[i]				4		3	prev[5] = 3
	prev[i]
结束	prev[i]	0	0	0	4	0	3

前驱结点初始化？？？

初始化：

	0	1	2	3	4	5
prev[i]	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$

邻接矩阵

$if(D[\ v \ ] < INFINITY)\ \ \ \ prev[\ v \ ] = 0;$

	0	1	2	3	4	5
prev[i]	$\infty$	$\infty$	0	$\infty$	0	0

结果：

	0	1	2	3	4	5
prev[i]	$\infty$	$\infty$	0	4	0	3

C++ 伪代码

for (int i = 0; i < G.vexnum; i++) {
    if (prev[i] == INFINITY) continue;
    int n = i;
    while (prev[n] != INFINITY) {
        path.push(n);               // 入栈
        n = prev[n];
    }
    path.push(0);
    while (!path.empty()) {
        path.pop();                 // 输出路径并出栈
    }
}

¶Floyd

Floyd 算法（有向无向 / 边权正负）

多源最短路径算法

$O(n^3)$

讨论有向带权图

对于稠密图，效率高于执行 $|v|$ 次 Dijkstra

引入 $map$ 矩阵

$map(i, j)$ 表示节点 $i$ 至节点 $j$ 最短路径的距离

对于每个节点 $k$ ，检查 $map(i, k) + map(k, j) < map(i, j)$

若成立，则 $map(i, j) = map(i, k) + map(k, j)$

主要步骤：

（1）初始化 $map$ 矩阵

若不相邻，则 $map[\ i \ ] [\ j \ ] = \infty$

若是相邻（即有边），则 $map[\ i \ ] [\ j \ ] = G.arcs[\ i \ ] [\ j \ ]$

若 $i = j$ ，$map[\ i \ ] [\ j \ ] = 0$

（2）分别以每个顶点为中介点，更新 $map$ 矩阵

for (k = 1; k <= n; k++)
    for (i = 1; i <= n; i++)
        for (k = 1; k <= n; k++)
            if (map[i][k] + map[k][j] < map[i][j])
                map[i][j] = map[i][k] + map[k][j];