拓扑排序（Topological sorting）

¶概念

对于一个有向无环图 $G = (V, E)$ 来说，其 拓扑排序 是 $G$ 中所有结点的一种线性次序
该次序满足如下条件：如果图 $G$ 包括边 $(u, v)$，则结点 u 在拓扑排序中处于结点 $v$ 的前面

¶基本想法

本质上是一种依赖关系

给定一个 DAG（有向无环图），如果从 $i$ 到 $j$ 有边，则认为 $j$ 依赖于 $i$ 。如果 $i$ 到 $j$ 有路径（ $i$ 可达 $j$ ），则称 $j$ 间接依赖于 $i$

拓扑排序的目标是将所有节点排序，使得排在前面的节点不能依赖于排在后面的节点

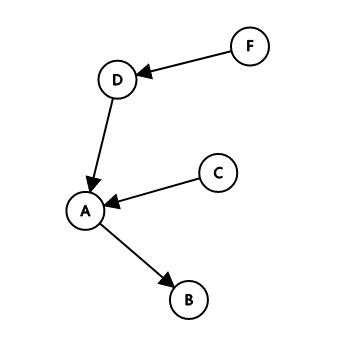
拓扑排序结果：FDCAB

入度最小的先遍历

（1）把入度为 $0$ 的顶点（无前驱）找到并打印
（2）删除入度为 $0$ 顶点，及其所有出边
（3）循环 (1)(2) 直至图为 NULL，即全部顶点均已输出，或是不存在入度为 $0$ 的顶点，这种情况则说明有向图中存在环

采用邻接表作为有向图的存储结构，且在头结点中增加一个存放顶点入度的数组（indegree）。入度为零的顶点即为没有前驱的顶点，删除顶点及以它为尾的弧的操作，则可换以弧头顶点的入度减 $1$ 来实现，为避免重复检测入度为零的顶点，可另设一栈暂存所有入度为零的顶点

下面是 C 语言描述的拓扑排序的 Kahn 算法

Status TopologicalSort(ALGraph G) {
    // 有向图 G 采用邻接表存储结构
    // 若 G 无回路，则输出 G 的顶点的一个拓扑序列并返回 OK，否则 ERROR
    FindInDegree(G, indegree);              // 对各顶点求入度 indegree[0..vernum - 1]
    InitStack(S);
    for (i = 0; i < G.vexnum; ++i)          // 建零入度顶点栈 S
        if (!indegree[i])   Push(S, i);     // 入度为 0 者进栈
    count = 0;                              // 对输出顶点计数
    while (!StackEmpty(S)) {
        Pop(S, i);  printf(i, G.vertices[i].data);  ++count;    // 输出 i 号顶点并计数
        for (p = G.vertices[i].firstarc; p; p = p->nextarc) {
            k = p->adjvex;                          // 对 i 号顶点的每个邻接点的入度减 1
            if (!(--indegree[k]))   Push(S, k);     // 若入度减为 0，则入栈
        } // for
    } // while
    if (count < G.vexnum)   return ERROR;           // 该有向图有回路
    else return OK;
} // TopologicalSort

对有 $n$ 个顶点和 $e$ 条弧的有向图，进行时间复杂度的分析：
求各顶点入度 $O(e)$ ，建零入度顶点栈 $O(n)$ ，
若无环，则每一个顶点进一次栈，出一次栈，入度减 $1$ 的操作在 while 语句中总共执行 $e$ 次
所以总的时间复杂度为 $O(n + e)$

C++ 伪代码

bool toposort() {
    q = new queue();
    for (i = 0; i < n; i++)
        if (in_deg[i] == 0) q.push(i);
    ans = new vector();
    while (!q.empty()) {
        u = q.pop();
        ans.push_back(u);
        for each edge(u, v) {
            if (--in_deg[v] == 0) q.push(v);
        }
    }
    if (ans.size() == n) {
        for (i = 0; i < n; i++)
            std::cout << ans[i] << std::endl;
        return true;
    } else {
    return false;
    }
}

下面的例子来自《算法导论》

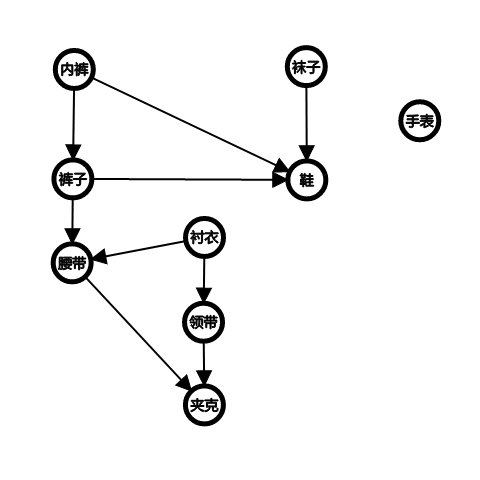
下图描述的是 Bumstead 教授每天早上起床穿衣所发生的事件的次序图，教授必须先穿某些衣服，才能再穿其他衣服，比如先穿袜子后才能再穿鞋，有些服饰则可以以任意顺序穿上，比如袜子和裤子之间可以以任意次序进行穿戴，在这个有向无环图中，有向边 $(u, v)$ 表明服装 u 必须在服装 v 之前穿上，对该图进行拓扑排序所获得的就是一种合理穿衣的次序

有向无环图的顶点	手表	袜子	内裤	裤子	鞋	腰带	衬衣	领带	夹克	ans（排序结果变化）
对各顶点求入度	0	0	0	1	3	2	0	1	2
建零入度顶点栈 S 入度为 0 者进栈	进栈	进栈	进栈				进栈
栈顶元素出栈							出栈			衬衣
邻接点入度减1 入度为 0 者进栈	0	0	0	1	3	1		入度为0 进栈	2
栈顶元素出栈								出栈		衬衣领带
邻接点入度减1 入度为 0 者进栈	0	0	0	1	3	1			1
栈顶元素出栈			出栈							衬衣领带内裤
邻接点入度减1 入度为 0 者进栈	0	0		入度为0 进栈	2	1			1
栈顶元素出栈				出栈						衬衣领带内裤裤子
邻接点入度减1 入度为 0 者进栈	0	0			1	入度为0 进栈			1
栈顶元素出栈						出栈				衬衣领带内裤裤子腰带
邻接点入度减1 入度为 0 者进栈	0	0			1				入度为0 进栈
栈顶元素出栈									出栈	衬衣领带内裤裤子腰带夹克
邻接点入度减1 入度为 0 者进栈	0	0			1
栈顶元素出栈		出栈								衬衣领带内裤裤子腰带夹克袜子
邻接点入度减1 入度为 0 者进栈	0				入度为0 进栈
栈顶元素出栈					出栈					衬衣领带内裤裤子腰带夹克袜子鞋
邻接点入度减1 入度为 0 者进栈	0
栈顶元素出栈	出栈									衬衣领带内裤裤子腰带夹克袜子鞋手表
邻接点入度减1 入度为 0 者进栈

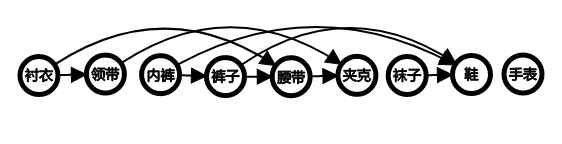
通过上述的排序过程得到了 Bumstead 教授对自己每天早上的穿衣进行的拓扑排序

当有向图中无环时，也可利用深度优先遍历进行拓扑排序，因为图中无环，则由图中某点出发进行深度优先搜索遍历时，最先退出 DFS 函数的顶点即出度为零的顶点，是拓扑有序序列中的最后一个顶点。由此按退出 DFS 函数的先后记录下来的顶点序列即为逆向的拓扑有序序列

———《数据结构》

OI Wiki 中的代码

vector<int> G[MAXN];  // vector 实现的邻接表
int c[MAXN];          // 标志数组
vector<int> topo;     // 拓扑排序后的节点

bool dfs(int u) {
  c[u] = -1;
  for (int v : G[u]) {
    if (c[v] < 0)
      return false;
    else if (!c[v])
      if (!dfs(v)) return false;
  }
  c[u] = 1;
  topo.push_back(u);
  return true;
}

bool toposort() {
  topo.clear();
  memset(c, 0, sizeof(c));
  for (int u = 0; u < n; u++)
    if (!c[u])
      if (!dfs(u)) return false;
  reverse(topo.begin(), topo.end());
  return true;
}

《入门经典》中的代码

int c[maxn];
int topo[maxn], t;
bool dfs(int u) {
    c[u] = -1;  // 访问标志
    for (int v = 0; v < n; v++) if (G[u][v]) {
        if (c[v] < 0)   return false;   // 存在有向环，失败退出
        else if (!c[v] && !dfs(v))  return false;
    }
    c[u] = 1; topo[--t] = u;
    return true;
}
bool toposort() {
    t = n;
    memset(c, 0, sizeof(c));
    for (int u = 0; u < n; u++)  if (!c[u])
        if(!dfs(u)) return false;
    return true;
}