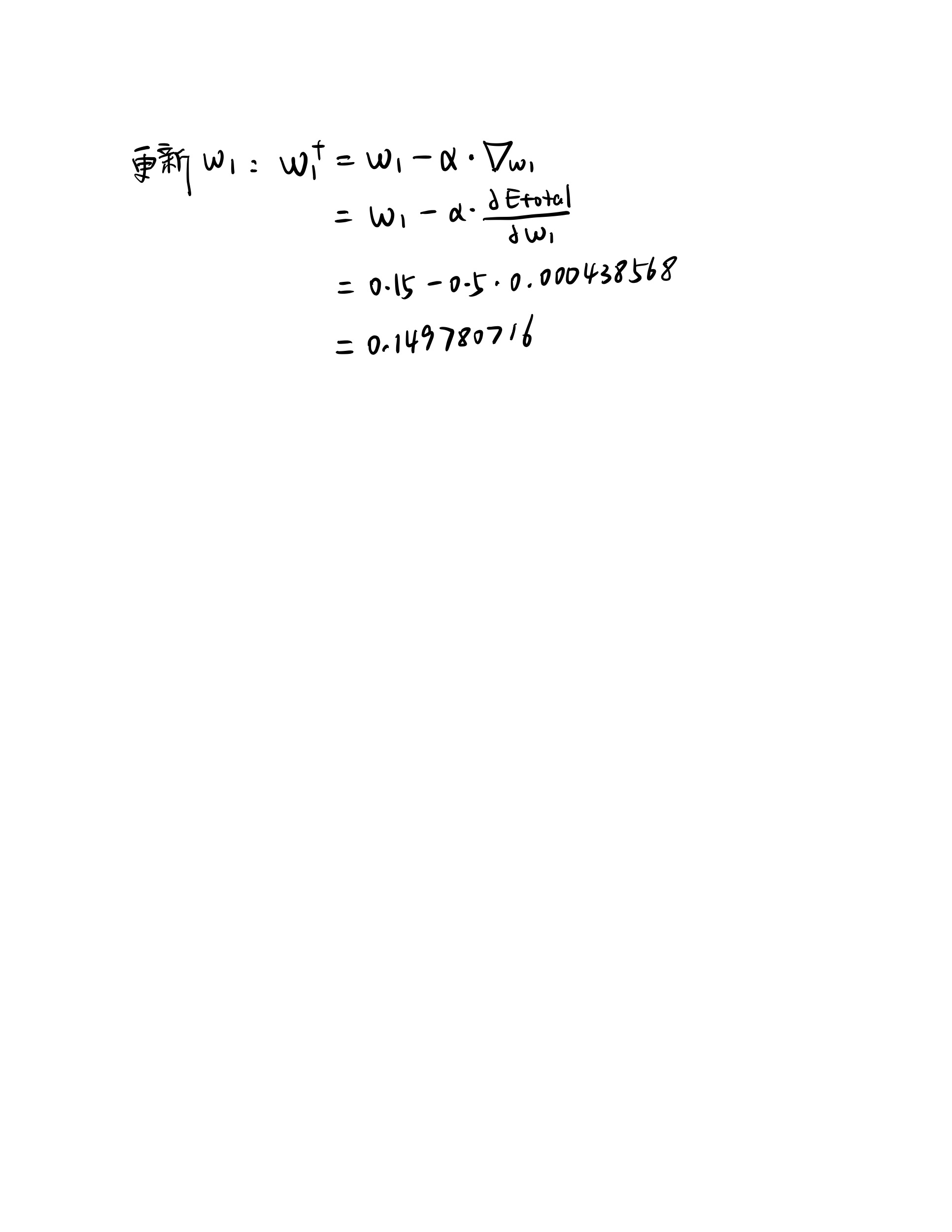本文将要介绍的这些问题涉及到的机器学习方法如下
线性回归 $~~~~$ 逻辑回归 $~~~~$ 朴素贝叶斯分类器 $~~~~$ 决策树
对偶问题 $~~~~$ 支持向量机 $~~~~$ 神经网络的反向传播
¶多元线性回归求解
多元线性回归试图学得 $h(x^{(i)}) = \sum\limits^{n}_{j=0} \theta_j x^{(i)}_j $,$\text{where } x^{(i)}_0 = 1$,使得 $h(x^{(i)}) \simeq y^{(i)}$,其中,$j = 1,2,…,n$,$n$ 为样本的特征数,$i = 1,2,…,m$,$m$ 为训练集的样本个数,采用最小二乘法,将代价函数矩阵化并对其求导,令导数等于 $0$,化简得到最小二乘估计的正规方程为
$$\boldsymbol{X}^\mathrm{T} \boldsymbol{X} \boldsymbol{\theta} = \boldsymbol{X}^\mathrm{T} \boldsymbol{y}\tag{1 - 1}$$求解正规方程,得到最终学得的多元线性回归模型的参数为
$$\boldsymbol{\theta} = (\boldsymbol{X}^\mathrm{T} \boldsymbol{X})^{-1} \boldsymbol{X}^\mathrm{T} \boldsymbol{y}\tag{1 - 2}$$其中,矩阵 $\boldsymbol{X}$ 与 矩阵 $\boldsymbol{y}$ 的结构为
$$ \boldsymbol{X}= \begin{bmatrix} x_0^{(1)} & x_1^{(1)} & \cdots & x_n^{(1)} \\ x_0^{(2)} & x_1^{(2)} & \cdots & x_n^{(2)} \\ \vdots & \vdots & \ddots & \vdots \\ x_0^{(m)} & x_1^{(m)} & \cdots & x_n^{(m)} \\ \end{bmatrix} , ~~ \boldsymbol{y} = \begin{bmatrix} y^{(1)} \\ y^{(2)} \\ \vdots \\ y^{(m)} \end{bmatrix} \tag{1 - 3} $$矩阵求逆
矩阵求逆常用的有三种方法,分别为待定系数法,初等行变换法,伴随矩阵法
待定系数法:
待定逆矩阵的所有元素,将原矩阵与逆矩阵作矩阵乘法,使其结果为单位矩阵
初等行变换法:
利用初等行变换,将 $(\boldsymbol A, \boldsymbol E)$ 变换为 $(\boldsymbol E, \boldsymbol B)$,矩阵 $\boldsymbol B$ 即为 $\boldsymbol A^{-1}$
伴随矩阵法:
利用公式 $\boldsymbol A^{-1} = \dfrac{1}{|\boldsymbol A|} \boldsymbol A^{*}$ 求得逆矩阵,其中伴随矩阵 $\boldsymbol A^{*} = [(-1)^{i+j}M_{ij}]^{\mathrm{T}}$,$M$ 为矩阵 $\boldsymbol A$ 中元素 $a_{ij}$ 的余子式
问题 1
给定某大学若干名学生身高(Height,单位:英寸 inch)与体重(Weight,单位:磅 pound)的数据,要求根据样本数据求得以身高预测体重的线性回归模型,并根据另一位同学的身高预测出他/她的体重(为了简化运算,给出示例,此处为单变量线性回归)
| 编号 | $i$ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Height/inch | $x_i$ | 63 | 64 | 66 | 69 | 69 | 71 | 71 | 72 | 73 | 75 |
| Weight/pound | $y_i$ | 127 | 121 | 142 | 157 | 162 | 156 | 169 | 165 | 181 | 208 |
将这 $10$ 组数据代入多元线性回归模型的参数公式进行计算,注意:$x^{(i)}_0 = 1$
根据数据得到
$$ \boldsymbol X = \begin{bmatrix} 1 & 63 \\ 1 & 69 \\ \vdots & \vdots \\ 1 & 75 \end{bmatrix} , ~~ \boldsymbol X^{\mathrm{T}} = \begin{bmatrix} 1 & 1 & \cdots & 1 \\ \\ 63 & 69 & \cdots & 75 \end{bmatrix} , ~~ \boldsymbol{y} = \begin{bmatrix} 127 \\ 121 \\ \vdots \\ 208 \end{bmatrix} \tag{P1 - 1} $$作矩阵乘法
$$ \boldsymbol{X}^\mathrm{T} \boldsymbol{X} = \begin{bmatrix} 10 & 693 \\ \\ 693 & 48163 \end{bmatrix} \tag{P1 - 2} $$对矩阵求逆
$$ (\boldsymbol{X}^\mathrm{T} \boldsymbol{X})^{-1} = \dfrac{1}{10 \times 48163 - 693^2} \begin{bmatrix} 48163 & -693 \\ \\ -693 & 10 \end{bmatrix} = \dfrac{1}{1381} \begin{bmatrix} 48163 & -693 \\ \\ -693 & 10 \end{bmatrix} \tag{P1 - 3} $$两次矩阵乘法
$$ (\boldsymbol{X}^\mathrm{T} \boldsymbol{X})^{-1} \boldsymbol{X}^\mathrm{T} = \dfrac{1}{1381} \begin{bmatrix} 4504 & 3811 & \cdots & -3812 \\ \\ -63 & -53 & \cdots & 57 \end{bmatrix} \tag{P1 - 4} $$$$ \boldsymbol\theta = (\boldsymbol{X}^\mathrm{T} \boldsymbol{X})^{-1} \boldsymbol{X}^\mathrm{T} \boldsymbol{y} = \dfrac{1}{1381} \begin{bmatrix} -368084 \\ \\ 8476 \end{bmatrix}= \begin{bmatrix} -266.5344 \\ \\ 6.1376 \end{bmatrix} \tag{P1 - 5} $$
求得结果
$$ w = -266.5344 + 6.1376 \cdot h \tag{P1 - 6} $$其中,$w$ 代表体重,$h$ 代表身高
¶二分类逻辑回归问题求解
设二分类问题的输出标记 $y \in \{0, 1\}$,用 $\text{sigmoid}$ 函数将线性回归模型的预测值转化为 $(0,1)$ 之间的值,即得到逻辑回归模型,可以认为逻辑回归模型的预测值是可能为 “1” 情况或者 “0” 情况的概率,若该概率大于 $0.5$ 即判定模型预测结果为其对应的情况
$\text{sigmoid}$ 函数
$$\text{sigmoid}(z) = \dfrac{1}{1 + e^{-z}} \tag{2 - 1}$$逻辑回归预测模型为
$$h_\theta(x) = g(\theta^T x) = \dfrac{1}{1 + e^{-\theta^T x}} \tag{2 - 2}$$我们选择用梯度下降法求得最大似然估计中 $\theta$ 的最优解,其迭代一次的操作为
$$ \begin{array}{lcl} & \text{(1)} & \boldsymbol H = \text{sigmoid}(\boldsymbol X \cdot \boldsymbol \theta) \\ & \text{(2)} & \boldsymbol\nabla = \boldsymbol X^{\mathrm{T}} (\boldsymbol H - \boldsymbol Y) ~~~~ \text{or} ~~~~ \boldsymbol\nabla = \dfrac{1}{m} \boldsymbol X^{\mathrm{T}} (\boldsymbol H - \boldsymbol Y) \\ & \text{(3)} & \boldsymbol \theta := \boldsymbol \theta - \alpha \cdot \boldsymbol\nabla \\ \end{array}\tag{2 - 3} $$其中,$\alpha$ 为预设的学习率,通常为 $0.01$、$0.001$ 等值
各矩阵的结构分别为
$$ \boldsymbol{X}_{m \times (n+1)} = \begin{bmatrix} x_0^{(1)} & x_1^{(1)} & \cdots & x_n^{(1)} \\ x_0^{(2)} & x_1^{(2)} & \cdots & x_n^{(2)} \\ \vdots & \vdots & \ddots & \vdots \\ x_0^{(m)} & x_1^{(m)} & \cdots & x_n^{(m)} \\ \end{bmatrix} , ~~ \boldsymbol{Y}_{m \times 1} = \begin{bmatrix} y^{(1)} \\ y^{(2)} \\ \vdots \\ y^{(m)} \end{bmatrix}\tag{2 - 4} $$$$ \boldsymbol{H}_{m \times 1} = \begin{bmatrix} H^{(1)} \\ H^{(2)} \\ \vdots \\ H^{(m)} \end{bmatrix} , ~~ ~~ ~~ ~~ \boldsymbol{\theta}_{(n+1) \times 1} = \begin{bmatrix} \theta_0 \\ \theta_1 \\ \vdots \\ \theta_n \end{bmatrix}\tag{2 - 5} $$
问题 2
给定某大学若干学生的 GPA 数值与其保研情况(只有 “是” 或 “否” 两种情况),请给出基于这些数据的逻辑回归模型,并根据该模型与另一位同学的 GPA 来预测他/她是否能够保研
| 编号 | $i$ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| GPA | $x_i$ | 3.81 | 3.70 | 3.67 | 3.63 | 3.56 | 3.45 | 3.35 | 3.18 | 2.77 | 2.5 |
| 保研情况 | 是/否 | 是 | 是 | 否 | 是 | 否 | 否 | 否 | 否 | 否 | 否 |
| 是/否对应1/0 | $y_i$ | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
我们当然不会用梯度下降法手动迭代成千上万次直至收敛,但是我们可以聚焦于其中的一次迭代过程
根据数据得到
$$ \boldsymbol X = \begin{bmatrix} 1 & 3.81 \\ 1 & 3.70 \\ 1 & 3.67 \\ \vdots & \vdots \\ 1 & 2.50 \end{bmatrix} , ~~ \boldsymbol{Y} = \begin{bmatrix} 1 \\ 1 \\ 0 \\ \vdots \\ 0 \end{bmatrix}\tag{P2 - 1} $$设初始的 $\boldsymbol\theta$ 矩阵为
$$ \boldsymbol{\theta} = \begin{bmatrix} 0 \\ \\ 0 \end{bmatrix}\tag{P2 - 2} $$则有
$$ \boldsymbol X \cdot \boldsymbol{\theta} = \begin{bmatrix} 0 \\ 0 \\ \vdots \\ 0 \end{bmatrix} , ~~ ~~ ~~ ~~ \boldsymbol H = \begin{bmatrix} 0.5 \\ 0.5 \\ \vdots \\ 0.5 \end{bmatrix}\tag{P2 - 3} $$$$ \boldsymbol\nabla = \boldsymbol X^{\mathrm{T}} (\boldsymbol H - \boldsymbol Y) = \begin{bmatrix} 2.00 \\ \\ 5.67 \end{bmatrix}\tag{P2 - 4} $$
设学习率 $\alpha$ 为 $0.01$,得到更新的 $\boldsymbol\theta$ 矩阵为
$$ \boldsymbol{\theta} = \begin{bmatrix} -0.02000 \\ \\ -0.05670 \end{bmatrix}\tag{P2 - 5} $$在计算机中迭代一百万次后得到 $\boldsymbol\theta^{\mathrm{T}} = \begin{bmatrix}-82.78829 & 22.73134 \end{bmatrix}$,此时若有一位同学的GPA为 $3.60$,根据此逻辑回归模型有
$$\text{hypothesis} = \dfrac{1}{1 + e^{-\theta^T x}} \approx 0.27779\tag{P2 - 6}$$可以预测,该同学不能保研
¶运用贝叶斯判定准则进行分类
对于分类任务来说,在所有相关概率都已知的理想情形下,贝叶斯决策论考虑如何基于这些概率和误判损失来选择最优的类别标记。假设有 $K$ 种可能的类别标记,即 $\gamma = \{ C_1, C_2, ... , C_K \}$,那么最小化分类器错误率的贝叶斯最优分类器为
$$ h(\boldsymbol x) = \mathop{\arg\max}\limits_{k \in \{ 1, \dots, K \}} \mathrm P(C_k ~|~ \boldsymbol x) \tag{3 - 1} $$即对每个样本 $\boldsymbol x$,选择能使后验概率 $\mathrm P(C_k ~|~ \boldsymbol x)$ 最大的类别标记
假设特征条件之间相互独立,上式基于贝叶斯公式推导得到的贝叶斯判定准则为
$$ \widehat y = \mathop{\arg\max}\limits_{k \in \{ 1, \dots, K \}} \mathrm P(C_k)\prod^{n}_{i=1} \mathrm P(x_i~|~C_k) \tag{3 - 2} $$其中,$n$ 为样本属性个数,$x_i$ 为 $\boldsymbol x$ 在第 $i$ 个属性上的取值
$p(C_k)$ 是好求的,当属性或者说特征为离散值时,$p(x_i~|~C_k)$ 亦不难求得,而当其为连续值时,则需考虑其概率密度函数,假定 $p(x_i~|~C_k) \sim \mathcal{N}(\mu_{C_k, i}, \sigma^2_{C_k, i})$,其中 $\mu_{C_k, i}, \sigma^2_{C_k, i}$ 分别是第 $k$ 类样本在第 $i$ 个属性上取值的均值和方差,则有
$$p(x_i~|~C_k) = \dfrac{1}{\sqrt{2\pi}\sigma_{C_k, i}}\exp\Big( -\dfrac{(x_i - \mu_{C_k, i})^2}{2\sigma^2_{C_k, i}} \Big) \tag{3 - 3}$$问题 3.1
Given a dataset about the relationship between whether Xiao E plays outside or not and the weather and temperature that day, if the weather tomorrow is overcast, and the temperature is mild, will he go out to play tomorrow?
| ID | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Weather | Sunny | Sunny | Overcast | Rainy | Rainy | Rainy | Overcast | Sunny | Sunny | Rainy | Sunny | Overcast | Overcast | Rainy |
| Temperature | Hot | Hot | Hot | Mild | Cool | Cool | Cool | Mild | Cool | Mild | Mild | Mild | Hot | Mild |
| Play | No | No | Yes | Yes | Yes | No | Yes | No | Yes | Yes | Yes | Yes | Yes | No |
二分类问题,先求先验概率与似然
$$\mathrm P(\text{play=Yes}) = \dfrac{9}{14}, ~~~~\mathrm P(\text{play=No}) = \dfrac{5}{14}\tag{P3.1 - 1}$$因为是离散值,很容易即可求得
$$\mathrm P(\text{weather=Overcast | play=Yes}) = \dfrac{4}{9} \tag{P3.1 - 2}$$ $$\mathrm P(\text{Temperature=Mild | play=Yes}) = \dfrac{4}{9} \tag{P3.1 - 3}$$ $$\mathrm P(\text{weather=Overcast | play=No}) = \dfrac{0}{5} \tag{P3.1 - 4}$$ $$\mathrm P(\text{Temperature=Mild | play=No}) = \dfrac{2}{5} \tag{P3.1 - 5}$$根据贝叶斯判定准则有
$$\mathrm P(\text{play=Yes | weather=Overcast, Temperature=Mild}) \\ \Longrightarrow \mathrm P(\text{play=Yes}) \cdot \mathrm P(\text{weather=Overcast | play=Yes})\cdot \mathrm P(\text{Temperature=Mild | play=Yes}) \\ = \dfrac{9}{14} \cdot \dfrac{4}{9} \cdot \dfrac{4}{9} = 0.1270 \tag{P3.1 - 6}$$ $$\mathrm P(\text{play=No | weather=Overcast, Temperature=Mild}) \\ \Longrightarrow \mathrm P(\text{play=No}) \cdot \mathrm P(\text{weather=Overcast | play=No})\cdot \mathrm P(\text{Temperature=Mild | play=No}) \\ = \dfrac{5}{14} \cdot \dfrac{0}{5} \cdot \dfrac{2}{5} = 0 \tag{P3.1 - 7}$$由于 $0.1270 > 0$,结论是,根据天气与温度情况,我们推断小 E 明天将会出去玩
在上面的计算过程中,$\mathrm P(\text{weather=Overcast | play=No}) = 0$,使得乘积结果一定为 $0$,于是其他属性携带的信息都被抹去,产生了零概率问题,于是我们在估计概率值时进行拉普拉斯平滑来解决这个问题
$$\mathrm P(\text{play=Yes}) = \dfrac{9+1}{14+2} = \dfrac{10}{16}, ~~~~\mathrm P(\text{play=No}) = \dfrac{5+1}{14+2} = \dfrac{6}{16} \tag{P3.1 - 7}$$ $$ \mathrm P(\text{weather=Overcast | play=Yes}) = \dfrac{4+1}{9+3} = \dfrac{5}{12} \tag{P3.1 - 8} $$ $$ \mathrm P(\text{Temperature=Mild | play=Yes}) = \dfrac{4+1}{9+3} = \dfrac{5}{12} \tag{P3.1 - 9} $$ $$ \mathrm P(\text{weather=Overcast | play=No}) = \dfrac{0+1}{5+3} = \dfrac{1}{8} \tag{P3.1 - 10} $$ $$ \mathrm P(\text{Temperature=Mild | play=No}) = \dfrac{2+1}{5+3} = \dfrac{3}{8} \tag{P3.1 - 11} $$ $$\mathrm P(\text{play=Yes | weather=Overcast, Temperature=Mild}) \\ \Longrightarrow \dfrac{10}{16} \cdot \dfrac{5}{12} \cdot \dfrac{5}{12} = 0.1085 \tag{P3.1 - 12}$$ $$\mathrm P(\text{play=No | weather=Overcast, Temperature=Mild}) \\ \Longrightarrow \dfrac{6}{16} \cdot \dfrac{1}{8} \cdot \dfrac{3}{8} = 0.0176 \tag{P3.1 - 13}$$结论一致
问题 3.2
给定一个西瓜数据集,请你用它训练一个朴素贝叶斯分类器,对测试例 “测一” 进行分类

首先估计类先验概率 $\mathrm P(C_k)$,显然有

然后,为每个属性估计条件概率 $\mathrm P(x_i~|~C_k)$

连续值处理,假设密度和含糖率满足正态分布,计算时应注意均值和方差

于是有

由于 $0.038 > 6.80\times 10^{-5}$,因此,朴素贝叶斯分类器将测试样本 “测一” 判别为 “好瓜”
在实践中,常通过取对数的方式将连乘转化为连加,以避免数值下溢
¶构造决策树及其剪枝策略
特征纯度的度量我们使用信息熵
$$\text{Entropy}(x) = -\sum^{n}_{i=0}P(x_i)\log_2P(x_i) \tag{4 - 1}$$信息熵可以衡量一个数据集的信息“纯度”。信息越纯,熵就越低;信息越混杂,熵就越高。
于是可以用信息增益来表示特征纯度的提升
$$\text{Information gain}(i) = \text{Entropy of parent table}~D~-\text{Sum}(\dfrac{n_k}{n} \cdot\\ \text{Entropy of each value}~k~\text{of subset table }S_i) \tag{4 - 2}$$即父亲节点的信息熵减去子节点上样本熵的加权平均数。在 $\text{ID3}$ 算法中,通过测量各种切分方案的信息增益,选择具有最大信息增益的切分方式,即可确定决策树上这一个父亲节点的切分。
问题 4
Based on above training data, we can induce a decision tree as the following:
CSDN 作者【天泽28】在关于周志华老师的《机器学习》(西瓜书)的笔记总结中对决策树模型介绍得很好,简单易懂,尽管文中有一些小错误,但是在评论区中都有提及,不影响整体阅读
决策树(decision tree)(一)——构造决策树方法
决策树(decision tree)(二)——剪枝
决策树(decision tree)(三)——连续值处理
决策树(decision tree)(四)——缺失值处理
¶拉格朗日函数与对偶形式求解带约束优化问题
对于优化问题
$$ \begin{array}{lcl} \min\limits_{\boldsymbol u} & & f(\boldsymbol u) \tag{5 - 1}\\ \text{ s. t.} & & g_i(\boldsymbol u) \le 0, ~~~~ i = 1,2,...,m~, \\ & & h_j(\boldsymbol u) = 0, ~~~~ j = 1,2,...,n~. \end{array} $$定义其拉格朗日函数为
$$ \mathcal{L}(\boldsymbol u, \boldsymbol\alpha, \boldsymbol\beta) := f(\boldsymbol u) + \sum^{m}_{i=1} \alpha_i g_i(\boldsymbol u) + \sum^{n}_{j=1} \beta_j h_j(\boldsymbol u) \tag{5 - 2} $$其中 $\alpha_i \ge 0$
式 (1) 描述的优化问题等价于
$$ \begin{array}{lcl} \min\limits_{\boldsymbol u}\max\limits_{\boldsymbol\alpha, \boldsymbol\beta} & & \mathcal{L}(\boldsymbol u, \boldsymbol\alpha, \boldsymbol\beta) \tag{5 - 3} \\ ~~~~\text{ s. t.} & & \alpha_i \ge 0, ~~~~ i = 1,2,...,m~. \\ \end{array} $$式 (3) 描述的优化问题在最优值处必须满足如下条件 ($\text{KKT}$ 条件)
- 主问题可行:$g_i(\boldsymbol u) \le 0, h_j(\boldsymbol u) = 0;$
- 对偶问题可行:$\alpha_i \ge 0;$
- 互补松弛:$\alpha_i g_i(\boldsymbol u) = 0.$
定义式 (1) 描述的优化问题的对偶问题
$$ \begin{array}{lcl} \max\limits_{\boldsymbol\alpha, \boldsymbol\beta}\min\limits_{\boldsymbol u} & & \mathcal{L}(\boldsymbol u, \boldsymbol\alpha, \boldsymbol\beta) \tag{5 - 4} \\ ~~~~\text{ s. t.} & & \alpha_i \ge 0, ~~~~ i = 1,2,...,m~. \\ \end{array} $$对偶问题是主问题的下界,即
$$ \max\limits_{\boldsymbol\alpha, \boldsymbol\beta}\min\limits_{\boldsymbol u} \mathcal{L}(\boldsymbol u, \boldsymbol\alpha, \boldsymbol\beta) \le \min\limits_{\boldsymbol u}\max\limits_{\boldsymbol\alpha, \boldsymbol\beta} \mathcal{L}(\boldsymbol u, \boldsymbol\alpha, \boldsymbol\beta) \tag{5 - 5} $$问题 5.1
Problem
$$ \begin{array}{lcl} \text{minimize:} & & x^2 + y^2 + 2z^2 \\ \text{subject to:} & & 2x + 2y - 4z \ge 8 \\ \end{array} $$$$2x + 2y - 4z \ge 8 \Longleftrightarrow 8 - 2x - 2y + 4z \le 0$$
The Lagrangian is:
$$ \mathcal{L}(x, y, z, \alpha) = x^2 + y^2 + 2z^2 + \alpha(8 - 2x - 2y + 4z) \tag{P5.1 - 1} $$Differentiating with respect to $x, y, z$
$$ \dfrac{\partial{\mathcal{L}}}{\partial x} = 2x - 2\alpha = 0 \tag{P5.1 - 2} $$ $$ \dfrac{\partial{\mathcal{L}}}{\partial y} = 2y - 2\alpha = 0 \tag{P5.1 - 3} $$ $$ \dfrac{\partial{\mathcal{L}}}{\partial z} = 4z + 4\alpha = 0 \tag{P5.1 - 4} $$We can conclude that
$$x = y = \alpha, ~~ z = -\alpha \tag{P5.1 - 5}$$Substituting this into $2x + 2y - 4z = 8$ gives
$$x = 1, ~~ y = 1, ~~ z = -1 \tag{P5.1 - 6}$$Optimal objective function value $ = 4$
问题 5.2
$$ \begin{array}{lcl} \text{minimize:} & & x_1^2 + x_2^2 \\ \text{subject to:} & & x_1 + x_2 \ge 4 \\ & & x_1, x_2 \ge 0 \end{array} $$Let
$$ X := \{ x \in \mathbb{R}^2 | x_1, x_2 \ge 0 \} = \mathbb{R}^+ \tag{P5.2 - 1} $$The Lagrangian is:
$$ \mathcal{L}(\boldsymbol x, \lambda) = x_1^2 + x_2^2 + \lambda(4 - x_1 - x_2) \tag{P5.2 - 2} $$The Lagrangian dual function:
$$ \begin{array}{lcl} \theta(\lambda) & = & \min\limits_{x \in X}\{ ~x_1^2 + x_2^2 + \lambda(4 - x_1 - x_2)~ \} \\ & = & 4\lambda + \min\limits_{x \in X}\{ ~x_1^2 + x_2^2 - \lambda x_1 - \lambda x_2~ \} \\ & = & 4\lambda + \min\limits_{x_1 \ge 0}\{ ~x_1^2 - \lambda x_1~ \} + \min\limits_{x_2 \ge 0}\{ ~x_2^2 - \lambda x_2~ \} \end{array} \tag{P5.2 - 3} $$For a fixed value of $\lambda \ge 0$,the minimum of $\mathcal{L}(\boldsymbol x, \lambda)$ over $x \in X$ is attained at
$$x_1(\lambda) = \dfrac{\lambda}{2}, ~~~~ x_2(\lambda) = \dfrac{\lambda}{2} \tag{P5.2 - 4}$$ $$\Longrightarrow \mathcal{L}(\boldsymbol x(\lambda), \lambda) = 4 \lambda - \dfrac{\lambda^2}{2} ~~~~ \forall \lambda \ge 0 \tag{P5.2 - 5}$$The dual function is concave and differentiable
We want to maximize the value of the dual function
$$ \dfrac{\partial{\mathcal{L}}}{\partial \lambda} = 4 - \lambda = 0 \tag{P5.2 - 6} $$This implies
$$ \lambda^* = 4, ~~~~ \theta(\lambda^*) = 8, ~~~~ \boldsymbol x(\lambda^*) = \boldsymbol x^* = (2, 2) \tag{P5.2 - 7} $$¶支持向量机求解线性二分类问题
给定一组数据 $\{ (\boldsymbol x_1, y_1), (\boldsymbol x_2, y_2), ... , (\boldsymbol x_m, y_m) \}$,其中 $\boldsymbol x_i \in \mathbb{R}^{d}$,$y \in \{ -1, 1 \}$,二分类任务的目标是希望从数据中学得一个假设函数 $h: \mathbb{R} \rightarrow \{ -1, 1 \}$,使得 $h(\boldsymbol x_i) = y_i$,即,线性二分类模型希望在特征空间找到一个划分超平面,将属于不同标记的样本分开,而 $\text{SVM}$ 进一步希望找到离各样本都比较远的划分超平面。
线性二分类模型:
找到一组合适的参数 $(\boldsymbol w, b)$,使得
线性支持向量机基本型
$$ \begin{array}{lcl} \mathop{\min}\limits_{\boldsymbol w, b} & & \dfrac{1}{2} \boldsymbol w^{\mathrm T} \boldsymbol w \\ \text{ s. t.} & & y_i(\boldsymbol w^{\mathrm T} \boldsymbol x_i + b) \ge 1, ~~~~ i = 1,2,...,m \end{array} \tag{6 - 2} $$线性支持向量机的拉格朗日函数为
$$\mathcal{L}(\boldsymbol{w}, b, \boldsymbol\alpha) = \dfrac{1}{2}\boldsymbol{w}^{\mathrm T} \boldsymbol w + \sum^{m}_{i=1} \alpha_i \Big(1 - y_i(\boldsymbol{w}^\mathrm{T} \boldsymbol{x_i} + b)\Big) \tag{6 - 3} $$其对偶问题为
$$ \begin{array}{lcl} \max\limits_{\boldsymbol\alpha}\min\limits_{\boldsymbol w, b} & & \dfrac{1}{2}\boldsymbol{w}^{\mathrm T} \boldsymbol w + \sum\limits^{m}_{i=1} \alpha_i \Big(1 - y_i(\boldsymbol{w}^\mathrm{T} \boldsymbol{x_i} + b)\Big) \\ ~~~~\text{ s. t.} & & \alpha_i \ge 0, ~~~~ i = 1,2,...,m~. \\ \end{array} \tag{6 - 4} $$因为式 $(6 - 4)$ 对 $(\boldsymbol w, b)$ 的优化属于无约束最小化问题,令偏导等于零,得到 $(\boldsymbol w, b)$ 的最优值
$$ \dfrac{\partial \mathcal{L}}{\partial w} = 0 \Rightarrow \boldsymbol w = \sum^{m}_{i=1} \alpha_i y_i \boldsymbol x_i, \tag{6 - 5} $$ $$ \dfrac{\partial \mathcal{L}}{\partial b} = 0 \Rightarrow \sum^{m}_{i=1} \alpha_i y_i = 0. \tag{6 - 6} $$将其代入式 $(6 - 4)$,消去 $(\boldsymbol w, b)$,得到线性支持向量机的对偶型
线性支持向量机的对偶问题等价于找到一组合适的参数 $\boldsymbol \alpha$,使得
$$ \begin{array}{lcl} \max\limits_{\boldsymbol\alpha} & & \sum\limits^{m}_{i=1} \alpha_i - \dfrac{1}{2}\sum\limits^{m}_{i=1}\sum\limits^{m}_{j=1} \alpha_i \alpha_j y_i y_j {\boldsymbol{x_i}}^\mathrm{T} \boldsymbol{x_j} \\ \text{ s. t.} & & \sum\limits^{m}_{i=1} \alpha_i y_i = 0, \\ & & \alpha_i \ge 0, ~~~~ i = 1,2,...,m. \\ \end{array} \tag{6 - 7} $$线性支持向量机的 $\text{KKT}$ 条件
- 主问题可行:$1 - y_i(\boldsymbol w^{\mathrm T} x_i + b) \le 0;$
- 对偶问题可行:$\alpha_i \ge 0;$
- 互补松弛:$\alpha_i(1 - y_i(\boldsymbol w^{\mathrm T} x_i + b)) = 0;$
线性支持向量机中,支持向量是距离划分超平面最近的样本,落在最大间隔边界上(即对偶变量 $\alpha_i > 0$ 对应的样本),支持向量机的参数 $(\boldsymbol w, b)$ 仅由支持向量决定,与其他样本无关
问题 6
给出
$$x_1 = \begin{bmatrix} 1 \\ 2 \end{bmatrix},y_1 = +1 \tag{P6 - 1}$$ $$x_2 = \begin{bmatrix} -1 \\ 2 \end{bmatrix},y_2 = +1 \tag{P6 - 2}$$ $$x_3 = \begin{bmatrix} -1 \\ -2 \end{bmatrix},y_3 = -1 \tag{P6 - 3}$$线性支持向量机的拉格朗日函数为
$$\mathcal{L}(\boldsymbol{w}, b, \boldsymbol\alpha) = \dfrac{1}{2}{\left \| \boldsymbol{w} \right \|}^2 - \sum^{m}_{i=1} \alpha_i \Big(y_i(\boldsymbol{w}^\mathrm{T} \boldsymbol{x_i} + b) - 1\Big) \tag{P6 - 4}$$令 $\dfrac{\partial{\mathcal{L}}}{\partial{\boldsymbol{w}}} = \boldsymbol{0}$,$\dfrac{\partial{\mathcal{L}}}{\partial{b}} = 0$,可得
$$\boldsymbol{w} = \sum^{m}_{i=1} \alpha_i y_i \boldsymbol{x_i} ~, \tag{P6 - 5}$$ $$\sum^{m}_{i=1} \alpha_i y_i = 0 ~. \tag{P6 - 6}$$由 (4) (5) (6) 式推导可知
$$\mathcal{L} = \sum^{m}_{i=1} \alpha_i - \dfrac{1}{2}\sum^{m}_{i=1}\sum^{m}_{j=1} \alpha_i \alpha_j y_i y_j {\boldsymbol{x_i}}^\mathrm{T} \boldsymbol{x_j} \tag{P6 - 7}$$将 (1) (2) (3) 式代入 (7) 式可得
$$\mathcal{L} = \alpha_1 + \alpha_2 + \alpha_3 - \dfrac{1}{2}\sum^{3}_{i=1}\begin{bmatrix} y_i(+1)\alpha_i \alpha_1 {\boldsymbol{x_i}}^\mathrm{T}\begin{bmatrix}1 \\2\end{bmatrix}\\ \\ +y_i(+1)\alpha_i \alpha_2 {\boldsymbol{x_i}}^\mathrm{T}\begin{bmatrix}-1 \\2\end{bmatrix}\\ \\ +y_i(-1)\alpha_i \alpha_3 {\boldsymbol{x_i}}^\mathrm{T}\begin{bmatrix}-1 \\-2\end{bmatrix} \end{bmatrix}$$$$\mathcal{L} = \alpha_1 + \alpha_2 + \alpha_3 - \dfrac{1}{2} \begin{bmatrix} {\alpha_1}^2 \begin{bmatrix}1,2\end{bmatrix} \begin{bmatrix}1 \\2\end{bmatrix} +\alpha_1\alpha_2 \begin{bmatrix}-1,2\end{bmatrix} \begin{bmatrix}1 \\2\end{bmatrix} -\alpha_1\alpha_3 \begin{bmatrix}-1,-2\end{bmatrix} \begin{bmatrix}1 \\2\end{bmatrix} \\ \\ +\alpha_2\alpha_1 \begin{bmatrix}1,2\end{bmatrix} \begin{bmatrix}-1 \\2\end{bmatrix} +{\alpha_2}^2 \begin{bmatrix}-1,2\end{bmatrix} \begin{bmatrix}-1 \\2\end{bmatrix} -\alpha_2\alpha_3 \begin{bmatrix}-1,-2\end{bmatrix} \begin{bmatrix}-1 \\2\end{bmatrix} \\ \\ -\alpha_3\alpha_1 \begin{bmatrix}1,2\end{bmatrix} \begin{bmatrix}-1 \\-2\end{bmatrix} -\alpha_3\alpha_2 \begin{bmatrix}-1,2\end{bmatrix} \begin{bmatrix}-1 \\-2\end{bmatrix} +{\alpha_3}^2 \begin{bmatrix}-1,-2\end{bmatrix} \begin{bmatrix}-1 \\-2\end{bmatrix} \end{bmatrix}$$
$$\mathcal{L} = \alpha_1 + \alpha_2 + \alpha_3 - \dfrac{1}{2}\Big( 5{\alpha_1}^2 + 5{\alpha_2}^2 + 5{\alpha_3}^2 + 6\alpha_1\alpha_2 + 10\alpha_1\alpha_3 + 6\alpha_2\alpha_3 \Big) \tag{P6 - 8}$$
对 (8) 式分别求偏导,并令偏导为零
$$\dfrac{\partial{\mathcal{L}}}{\partial{\alpha_1}} = 1 - 5\alpha_1 - 3\alpha_2 - 5\alpha_3 = 0 \tag{P6 - 9}$$ $$\dfrac{\partial{\mathcal{L}}}{\partial{\alpha_2}} = 1 - 5\alpha_2 - 3\alpha_1 - 3\alpha_3 = 0 \tag{P6 - 10}$$ $$\dfrac{\partial{\mathcal{L}}}{\partial{\alpha_3}} = 1 - 5\alpha_3 - 5\alpha_1 - 3\alpha_2 = 0 \tag{P6 - 11}$$由 (6) (9) (10) (11) 求得
$$\alpha_2 = \alpha_3 = \dfrac{1}{8} ~~,~~ \alpha_1 = 0 \tag{P6 - 12}$$将上式代入 (5) 式得
$$ \begin{array}{lcl} \boldsymbol{w} & = & \sum\limits^{m}_{i=1} \alpha_i y_i \boldsymbol{x_i} \\ \boldsymbol{w} & = & 0\begin{bmatrix} 1 \\ 2 \end{bmatrix} +\dfrac{1}{8}\begin{bmatrix} -1 \\ 2 \end{bmatrix} -\dfrac{1}{8}\begin{bmatrix} -1 \\ -2 \end{bmatrix} & = & \begin{bmatrix}~~ 0 ~~\\ \\ ~~\dfrac{1}{2}~~ \end{bmatrix} \end{array} $$可得
$$\boldsymbol{w} = \begin{bmatrix}~~ 0 ~~\\ \\ \dfrac{1}{2} \end{bmatrix} \tag{P6 - 13}$$由线性支持向量机的 $\text{KKT}$ 条件
$$\alpha_i \Big(y_i(\boldsymbol{w}^\mathrm{T} \boldsymbol{x_i} + b) - 1 \Big) = 0 \tag{P6 - 14}$$再将 (1) 式代入得
$$ \begin{array}{r} {y_i(\boldsymbol{w}^\mathrm{T} \boldsymbol{x_i} + b) - 1 = 0 }\\ {\boldsymbol{w}^\mathrm{T} \boldsymbol{x_i} + b - 1 = 0} \\ {\begin{bmatrix} 0, \dfrac{1}{2} \end{bmatrix} \begin{bmatrix} 1 \\ 2 \end{bmatrix} +b-1 = 0} \\ {b = 0} \end{array} $$可得
$$b=0\tag{P6 - 15}$$由 (13) (15) 知该线性二分类模型的划分超平面为
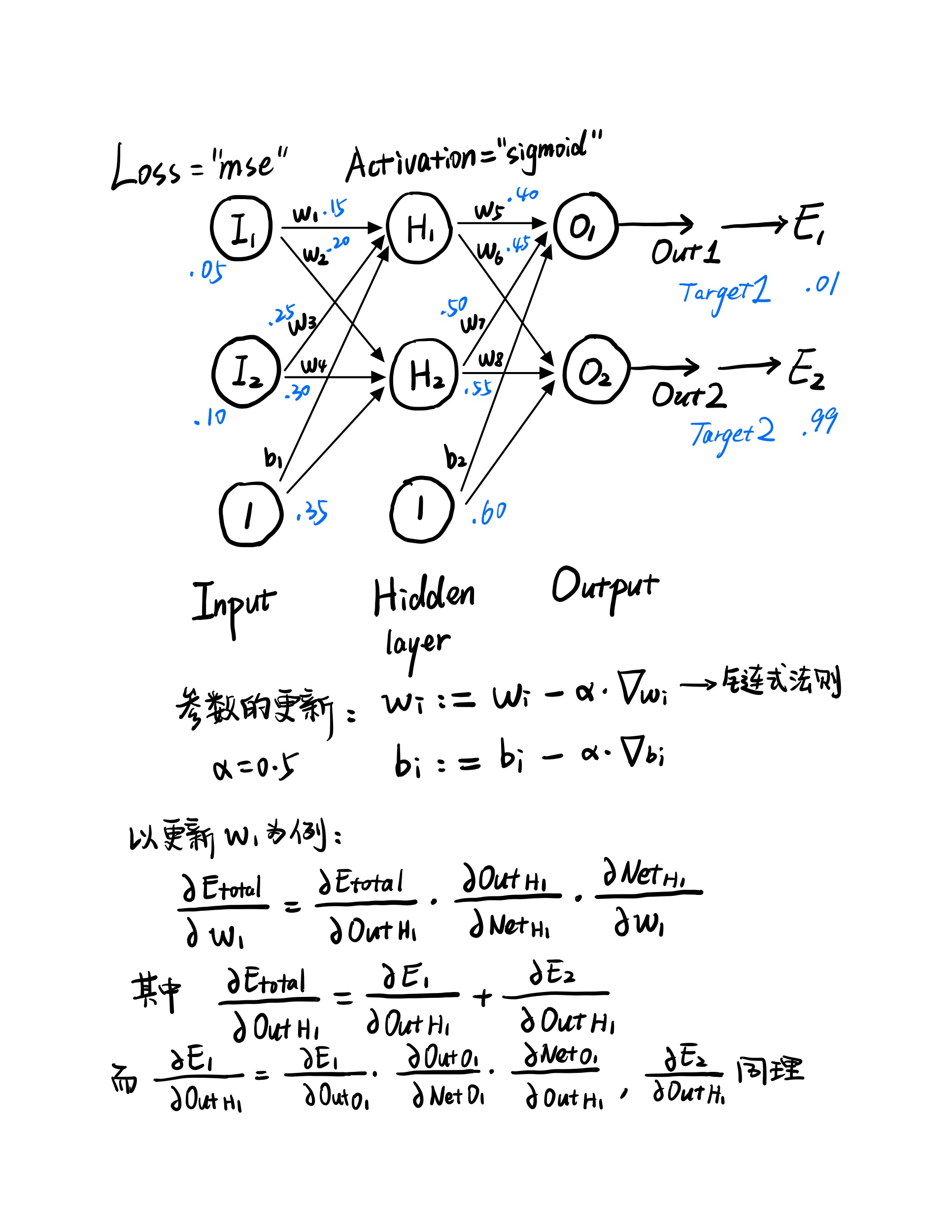
$$\boldsymbol{w}^\mathrm{T} \boldsymbol{x} + b = 0 ~, ~~~~~~~~\text{where}~~~~\boldsymbol{w} = \begin{bmatrix}~~ 0 ~~\\ \\ \dfrac{1}{2} \end{bmatrix}, ~b = 0 ~.\tag{P6 - 16}$$¶神经网络的误差反向传播法
-
神经网络的前向传播(Forward Propagation)
- 前向传播就是从input,经过一层层的layer,不断计算每一层的z和a,最后得到输出y^ 的过程,计算出了y^,就可以根据它和真实值y的差别来计算损失(loss)。
-
神经网络的反向传播(Backward Propagation)
- 反向传播就是根据损失函数L(y^,y)来反方向地计算每一层的z、a、w、b的偏导数(梯度),从而更新参数。
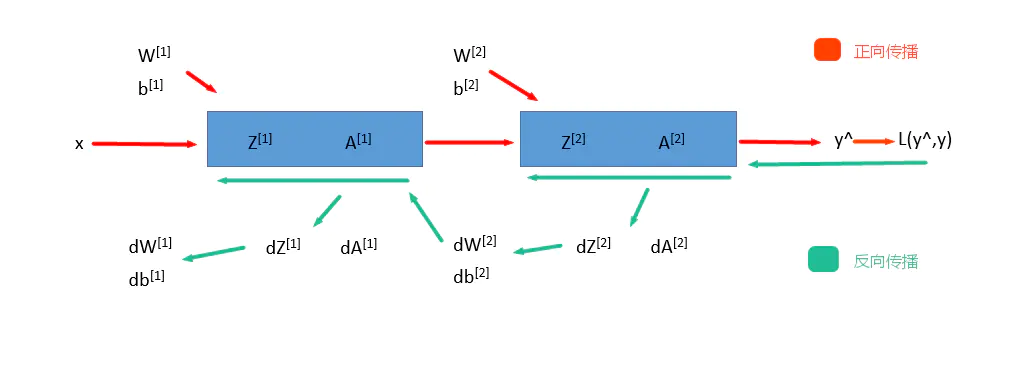
每经过一次前向传播和反向传播之后,参数就更新一次,然后用新的参数再次循环上面的过程。这就是神经网络训练的整个过程。