b站视频链接：北京理工大学ACM冬季培训课程
 课程刷题地址 2020BIT冬训-字符串入门但是没得密码。。。
本篇博文为看视频学习时的记录与自己的一些总结

字符串入门

¶基础约定与定义

记号 $\sum$ 表示字符集。字符串中的字符一定在字符集内。
$|s|$ 表示字符串 $s$ 的长度。$s[i](0 \le i < |s|)$ 表示字符串 $s$ 中的第 $(i+1)$ 个字符。
$s[l \dots r](0 \le l,r < |s|)$ 表示由串 $s$ 中下标为 $l$ 的字符到下标为 $r$ 的字符所组成的子串。特别地，若 $l > r$，则 $s[l \dots r]$ 为一空串。
对于两个字符串 $s$ 和 $t$，定义 $s$ 与 $t$ 相等（匹配）当且仅当 $|s| = |t|$ 且 $s[i] = t[i]$，$0 \le i < |s|$。
记 $pre_s[i]$ 表示 $s[0 \dots i]$，称为 $s$ 的前缀 $i$；$suf_s[i]$ 表示 $s[i \dots |s|-1]$，称为 $s$ 的后缀 $i$。
对于两个串 $s$ 和 $t$，定义 $LCP(s,t)$ 为 $s$ 与 $t$ 的最长公共前缀的长度。

¶构造与赋值

string s1();                // s1 = ""
string s2("Hello");         // s2 = "Hello"
string s3(4, 'K');          // s3 = "KKKK"
string s4("12345", 1, 3);   // s4 = "234", 即 "12345" 的从下标 1 开始，长度为 3 的子串

1
2
3

string s1;                  
s1 = "Hello";               // s1 = "Hello"
s2 = 'K';                   // s2 = "K"

¶String 成员函数

字符串长度 length 函数

String 对象支持 + 和 +=，append（在后面添加内容）
s1.append(s2)
支持比较运算符的比较
支持 compare 函数比较
s1.compare(s2)
支持 substr 函数求子串
s2 = s1.substr(2,4)
s1.empty() 判断是否为空

find: 从前往后查找子串或字符出现的位置。
rfind: 从后往前查找子串或字符出现的位置。
find_first_of: 从前往后查找何处出现另一个字符串中包含的字符。例如：
s1.find_first_of(“abc”); // 查找 s1 中第一次出现 “abc” 中任一字符的位置
find_last_of: 从后往前查找何处出现另一个字符串中包含的字符。
find_first_not_of: 从前往后查找何处出现另一个字符串中没有包含的字符。
find_last_not_of: 从后往前查找何处出现另一个字符串中没有包含的字符。

String 支持 insert
支持 replace
支持 erase
支持 substr 提取出子串
支持 push_back(char c)

¶字符串哈希

字符串哈希
STRING HASH
处理子串匹配的有力工具

¶什么是哈希？

哈希又称为散列，在计算机科学中表示一个将某个对象映射到某个整数值的过程。执行此映射的函数称为哈希函数。
由于计算机在检索数据时仅能检索数字量，哈希的引入为检索、匹配任意对象带来了方便。
字符串哈希 即为将一个字符串映射到某个整数的过程。字符串哈希函数在数学形式上即为某个函数 $f: S \rightarrow \mathbb{Z}$，其中 $S$ 为字符集上的全体字符串集合。

¶哈希函数的特点

哈希函数的函数值随输入的不同，其在值域内的分布是大致均匀的。
对输入量的微小改动也会引起哈希函数值的巨大变化。
对于同一个输入对象，其哈希值是唯一的。
不同的对象被哈希函数映射到同一个整数值（“冲突”、“碰撞”）的可能性是存在的，但其发生的概率是较小的。只有针对特定哈希算法的、经过精心挑选的字符串才会造成大概率的碰撞。
由第 4 个特点，若两字符串的哈希值相同，我们一般认为这两个字符串相同。

¶常用字符串哈希函数

在字符串匹配问题中，常用如下函数作为字符串哈希函数：

$$Hash(s) = \sum_{i=0}^{|s|-1} s[i] \cdot p^i，$$

其中 $p$ 是一个常数（通常取质数）。

定义 $Hash_s(i)$ 表示串 $s$ 的后缀 $i$ 的哈希值。则易知：

$$
Hash_s(i) =
\begin{cases}
0, & i=|s| \
Hash_s(i+1) \cdot p + s[i], & 0 \le i < |s|
\end{cases}
$$

定义 $Hash_s(i, L)$ 表示串 $s[i \dots i + L-1]$ 的哈希值。则易知：

$$Hash_s(i,L) = Hash_s(i) - Hash_s(i+L) \cdot p^L$$

在实际应用中，常将哈希值定义为 unsigned long long 型，并在运算过程中令其自由溢出（相当于对 $2^{64} - 1$ 取模）。

$
Hash_s(i) =
\begin{cases}
0, & i=|s| \
Hash_s(i+1) \cdot p + s[i], & 0 \le i < |s|
\end{cases}
$
$Hash_s(i,L) = Hash_s(i) - Hash_s(i+L) \cdot p^L$

由上面两式可以推出：

串 $s$ 的相邻子串（$s[i \dots j]$ 与 $s[i+1 \dots j+1]$ 为 $s$ 的一对相邻子串）的哈希函数值可以在 $O(1)$ 的时间内转移计算。

$$Hash_s(i,L) = Hash_s(i+1,L) \cdot p - s[i+L] \cdot p^L + s[i]$$

¶如何使用字符串哈希执行字符串匹配？

【例】给定一个模式串 $t$。给定 $q$ 组询问，每组询问给定一个待匹配串 $s$。对于每组询问，分别回答给定的待匹配串 $s$ 是否包含串 $t$ 作为子串。
【方法1】暴力。
时间复杂度：$O(Q|t||s|)$。
【方法2】字符串哈希。
首先，预处理串 $t$ 的哈希值。时间复杂度：$O(t)$。
对于每个询问，针对串 $s$ 中的每个长度为 $|t|$ 的子串，计算其子串哈希值并与模式串 $t$ 的哈希值进行比较。由于相邻子串间的子串哈希值可以在 $O(1)$ 的时间复杂度内进行转移，故该步骤的时间复杂度为 $O(Q|s|)$。
总体时间复杂度：$O(Q|s|+|t|)$。

【例】给出 N 个数，要求把其中重复的去掉，只保留第一次出现的数。
例如，给出的数为 1 2 18 3 3 19 2 3 6 5 4，其中 2 和 3 有重复，去除后的结果为 1 2 18 3 19 6 5 4。
对于 100% 的数据，1 <= N <= 50000，给出的数在 32 位无符号整数范围内。

【方法1】sort
【方法2】平衡树（可以自己手写 or set or map）
【方法3】Hash（把数字当成字符）

【例】小 Q 定义，若两个字符串是相似的，当且仅当这两个字符串等长且恰好只有一位不同。例如 “Penguin1” 和 “Penguin2” 是相似的，但 “Penguin1” 和 “2Penguin” 不是相似的。而小 Q 想知道，在给定的 N 个字符串中，有多少对是相似的。
为了简化你的工作，小 Q 给你的 N 个字符串长度均等于 L，且只包含大小写字母、数字、而且不存在两个相同的账户名称。
N <= 30000, L <= 200.

枚举删去某一位。然后算出 hash 表，求重复数字的方法可参考上一例题
枚举删去某一位后，计算一个字符串 Hash 值朴素做法是 $O(L)$，这样复杂度是 $O(L(NL + N \log N))$
再枚举删除一位之后，利用子串的拼接做到计算一个字符串的 hash 值要做到 $O(1)$，这样的复杂度是 $O(L(N+N \log N))$

¶字典树

字典树 TRIE 前缀树

字典树要解决的问题

给定一个字符串集合 $S$，给定 $Q$ 个询问，每个询问给定一个串 $t$。对于每个询问，要求回答给定的串 $t$ 是否为集合 $S$ 中某个字符串的前缀。

【方法1】暴力。
时间复杂度：$O(Q|t||S|)$。

【方法2】字典树。
时间复杂度：$O(Q|t| + \sum_{s \in S}|s|)$

在使用朴素暴力方法解决原问题时，我们可以发现，每次对集合 $S$ 中的一个串进行匹配时，要匹配的字符序列都是一样的：都是串 $t$ 的字符序列。我们应该想办法实现仅对串 $t$ 的字符序列匹配一次便得出答案。

字典树的基本思想和人类做上述匹配问题的思想很近似。考虑一个含有三个串 “aaa”、“aba” 和 “baa” 的字符串集合 $S$。当串 $t$ 为 “aaa” 时：

首先尝试匹配串 $t$ 的第一个字符 $a$，注意到 $S$ 中的第三个串的第一个字符为 $b$，因此第三个串一定不匹配，匹配串只可能在第一个串和第二个串间。
然后尝试匹配串 $t$ 的第二个字符 $a$，注意到 $S$ 中的第二个串的第二个字符为 $b$，因此第二个串一定不匹配，第三个串在上一轮匹配中已经被我们舍弃，不予考虑。

以此类推。

字典树巧妙的利用树结构来对上述 “选择还能够匹配的字符串” 这一过程进行优化。

假设 $S = { \text{ “hello”, “how”, “what”, “holy”, “hole” } }$。则对 $S$ 构造字典树如下：

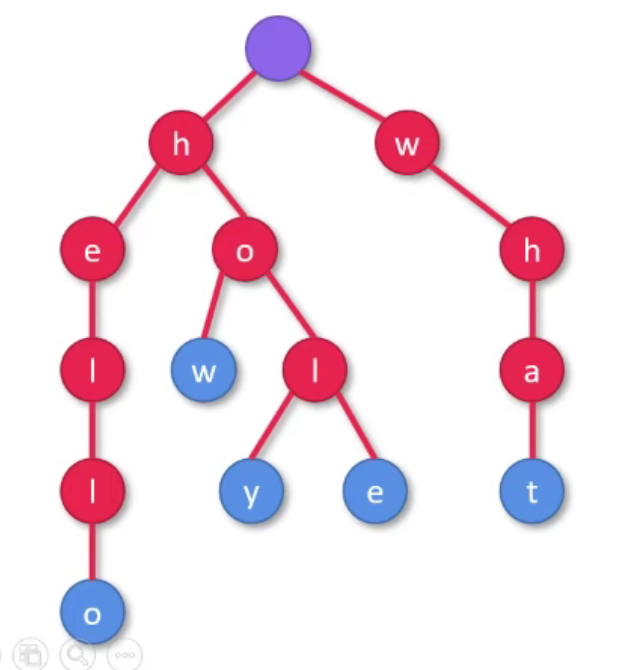
特点：

根结点到树上每个节点路径上的字母构成这个节点代表的字符串（根代表空字符串）；
叶子对应的字符串即为集合 $S$ 内的某个字符串；
不难看出，字典树的空间效率非常高。这是因为字典树充分利用了集合 $S$ 中的字符串的公共前缀部分。字典树的空间复杂度为 $O(\sum_{s \in S} |s|)$

字典树代码：

int tree[maxn][30];         // 小写字母 26 个
int tot;
void insert_(char *str)
{
    int len = strlen(str);
    int root = 0;
    for (int i = 0; i < len; i++)
    {
        int id = str[i] - 'a';
        if (!tree[root][id]) tree[root][id] = ++tot;
        root = tree[root][id];
    }
}

int find_(char *str)
{
    int len = strlen(str);
    int root = 0;
    for (int i = 0; i < len; i++)
    {
        int id = str[i] - 'a';
        if (!tree[root][id]) return 0;
        root = tree[root][id];
    }
    return root;
}

关于字典树上的一些符号约定

为了后文阐述方便，约定一些字典树上的符号含义：

对于字典树上一节点 p，记 $str§$ 表示从字典树根结点到节点 $p$ 路径上的字符组成的字符串。
对于一字符串 $s$，若 $s$ 包含在字典树中，记 $trienode(s)$ 表示串 $s$ 在字典树上对应的节点。
对于一字符串 $s$，若 $trienode(s)$ 在字典树上某节点 $p$ 的子树中，称串 $s$ 穿过节点 $p$。

易知，若串 $s$ 穿过节点 $p$，则 $str§$ 为 $s$ 的前缀。

【例】Ignatius 最近遇到一个难题，老师交给他很多单词（只有小写字母组成，不会有重复的单词出现），现在老师要他统计出以某个字符串为前缀的单词数量（单词本身也是自己的前缀）。

code here

PROBLEM：FIND MAX XOR SUM

给定 $n$ 个数 $a_1, a_2, \dots, a_n$。求 $\mathop{\max}\limits_{1 \le i, j \le n} { a_i \ \text{XOR} \ a_j }$。其中 $\text{XOR}$ 代表按位异或操作。

【方法1】暴力。
时间复杂度：$O(n^2)$。

【方法2】二进制字典树。
时间复杂度：$O(\log \mathop{\max}\limits_{1 \le i \le n} a_i)$

不妨将给定的数拆分成二进制位进行考虑。
贪心性质是显然的：答案的二进制表示下高位上 $1$ 越多，答案应该越大。
$\text{XOR}$ 得到 $1$，当且仅当输入为一个 $0$ 和一个 $1$。
对给定的所有数按照其二进制表示构造一颗字典树（此时字典树为一颗二叉树）。维护两个指针，进行 双指针 DFS 。每一步都贪心地尽量选择一个指针走向 $0$，一个指针走向 $1$。
双指针 DFS 过程中维护答案即可。

双指针 DFS 是树形字符串数据结构（字典树、自动机等）上的常用技巧。

PROBLEM：FIND MAX XOR SUM PLUS

给定 $n$ 个数 $a_1, a_2, \dots, a_n$。求 $\mathop{\max}\limits_{1 \le i, j \le n} { a_i \ \text{XOR} \ a_{i+1} \ \text{XOR} \ \dots \ \text{XOR} \ a_j }$。其中 $\text{XOR}$ 代表按位异或操作。

注意到 $\mathop{\text{XOR}}\limits_{i \le k \le j} a_k = \bigg(\mathop{\text{XOR}}\limits_{1 \le k < i} a_k \bigg) \text{XOR} \bigg( \mathop{\text{XOR}}\limits_{1 \le k \le j} a_k \bigg) $，即异或前缀和的性质：

$$sum[l, r] = A[l] \text{ xor } A[l + 1] \dots \text{ xor } A[r] = S[r] \text{ xor } S[l - 1]$$

预处理数组 ${ a_i }$ 的异或前缀和。随后问题转化为 FIND MAX XOR SUM