Cloud_Player's Notes
0%

拓扑排序与最短路

发表于 更新于
本文字数： 2k 阅读时长 ≈ 2 分钟

b站视频链接：北京理工大学ACM冬季培训课程
课程刷题地址 2020BIT冬训-拓扑排序&&最短路 Password: DijkstraduzuoDaiKeSiChua
本篇博文为看视频学习时的记录与自己的一些总结

拓扑排序与最短路

拓扑排序

所谓拓扑排序，是指将一个有向无环图 $G$ 的所有顶点排成一个线性序列，使得有向无环图 $G$ 的边集 $E$ 中的任意一条边 $\left\langle u, v \right\rangle$，始终满足 $u$ 出现在 $v$ 的前面

从离散数学的角度来说，拓扑排序是由某个集合上的一个偏序得到该集合上的一个全序的过程，直观地看，偏序指集合中仅有部分成员可比较，而全序指集合中全体成员之间均可比较，这个全序也称为拓扑有序

有向无环图 DAG

  • 什么是有向无环图
  • $(b)$ $©$ 皆为有向无环图，$(a)$ 不为有向无环图

拓扑（有）序

  • 在潜入类游戏中，一些敌人互相可以看到，需要暗杀掉所有人而不被发现，一个可行的暗杀序列，就是一个拓扑序
  • 在大学选课时，有些课程存在先修课，就是说你必须上完它的前置课程，你才能够开始这门课程，一个可行的选课序列，就是一个拓扑序
  • 有向无环图是存在拓扑序的充要条件

算法描述与实现

  • 在有向无环图中找到一个没有前驱的结点（或者说是入度为 0 的结点）输出
  • 然后从图中将此结点删除并且删除以该结点为尾的弧
  • 如果所有结点都已输出，则程序结束；否则，返回步骤一

拓扑排序的一个 C++ 实现（不是一定要用队列）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
int vis[maxn];                          // 没有 vis 数组会引发什么错误
int deg[maxn];                          // 统计点 i 的度数
vector<int> g[maxn];
queue<int> q;                           // 把所有入度为 0 的点先扔到一个队列里
bool toposort() {
    int num = 0;
    while (!q.empty()) {                // 队列非空
        int now = q.front(); q.pop();   // 取队首点 P
        num++;
        for (auto to : g[now]) {        // 访问 P 的所有相邻点 Q，将其入度减 1
            if (vis[to]) continue;
            else {
                deg[to]--;
                if (!deg[to]) {
                    vis[to] = 1;
                    q.push(to);         // 若 Q 此时入度为 0，Q 入列
                }
            }
        }
    }                                   // 出列顺序就是一个拓扑序
    if (num == n) return true;
    else return false;                  // 队列空时，拓扑序列没达到顶点数，则不存在拓扑序
}

应用

模板题 + 简单题

有 $N$ 个队参加比赛（$1 \le N \le 500$），队伍编号依次为 $1$，$2$，$3$，$\dots$，$N$，一共有 $M$ 场比赛，比赛结束后，裁判委员会要将所有的参赛队伍依次排名，但现在裁判委员会只知道每场比赛的结果，比如编号为 $1$ 的队伍赢了编号为 $2$ 的队伍，在输入中用 $1\ 2$ 表示，则排名时队 $1$ 应该在队 $2$ 之前，编写程序，确定最终的排名，若不唯一，则编号小的队伍在前

临近春节，老板决定为每个员工发红包，为了图吉利，每个员工的红包不少于 $888$ 且为整数，一些员工可能提出自己的红包金额应该比某位员工的红包金额要大的要求，在输入中 $1\ 2$ 表示编号为 $1$ 的员工认为自己的红包要比编号为 $2$ 的员工大，员工数 $n \le 10000$，提出的要求数 $m \le 20000$，老板希望满足所有员工的要求的同时发出红包的总金额最小，编写程序计算总金额并输出，若不可能满足所有员工的要求，输出 $-1$ 即可（提示：反向建图，拓扑排序）

最短/长路

用拓扑排序快速求有向无环图的最短路

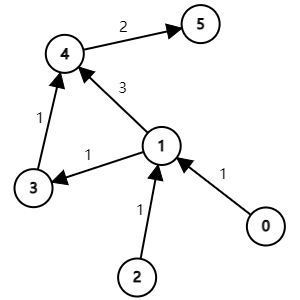
求上图中，2 到 5 的最短路

  • 仿照 BFS，定义 dis 数组表示某个点到起点的距离
  • 全部初始化为正无穷，dis[起点] = 0
  • 在拓扑排序的过程中，不断执行
    dis[to] = min(dis[to], dis[from] + value)
  • 当拓扑排序完成的时候，也就求出了最短路的长度
  • 同理，可以求最长路
  • 动态规划实际上是在一张有向无环图上进行拓扑排序的过程

其他

拓扑排序经常结合其他算法一起出现
比如：拓扑 + 层次遍历、拓扑 + 并查集 等等

最短路

单源最短路

BFS 的局限

SPFA 算法

堆优化的 Dijkstra

Dijkstra

Bellman-Ford

多源最短路

Floyd-Warshall

总结

  • Dijkstra 与 Bellman-Ford ：分别被堆优化 Dijkstra 与 SPFA 干掉了，实际是不用的
  • 单源最短路问题：堆优化 Dijkstra 与 SPFA
    • 正权图：必须堆优化 Dijkstra，算法复杂度为 $O(E \log E)$
    • 负权图：只能 SPFA
    • 负环：没有最短路，SPFA 可以发现负环
  • 多源最短路问题：
    • Floyd 算法