Cloud_Player's Notes
0%

简单数据结构

发表于 更新于
本文字数： 5.2k 阅读时长 ≈ 5 分钟

b站视频链接：北京理工大学ACM冬季培训课程
课程刷题地址 2020BIT冬训-简单数据结构 但是没得密码。。。
本篇博文为看视频学习时的记录与自己的一些总结

简单数据结构

前缀和

定义

若 $S[i] = \sum\limits^{i}_{j=1} A[j]$，则称 $S$ 是 $A$ 的前缀和

前缀和是一种重要的预处理，能大大降低查询的时间复杂度。可以简单理解为“数列的前 $n$ 项的和”。有以下性质：

$$sum[l, r] = \sum^{r}_{i=1} A[i] = S[r] - S[l - 1]$$

  • 给定 $A$ 数列，长度为 $n$，$m$ 次询问，每次询问 $L_i, R_i$ 求 $\sum^{R_i}_{j=L_i} A[j]$（区间和）
1
2
3
4
5
6
7
//用 O(n) 前缀和预处理，O(m) 询问
for(int i = 1; i <= n; ++i) sum[i] = sum[i - 1] + a[i]; //O(n)
while(m--)  //O(m)
{
    int L, R; scanf("%d%d", &L, &R);
    printf("%d\n", sum[R] - sum[L - 1]);
}
  • 给定 $A$ 数列，长度为 $n$，先 $m$ 次修改，再 $q$ 次询问，每次修改为在 $A$ 数组的区间 $[ L_i, R_i ]$ 内都加上一个数 $x$，即 $A[j] += x, j \in [ L_i, R_i ], j \in R$， 每次询问 $L_i, R_i$ 求 $\sum^{R_i}_{j=L_i} A[j]$（区间和）
    在这里实际上引入了差分的思想，由于要进行 $m$ 次的修改，每次修改都是对一个区间长度内的所有元素做加法，这样明显是一个不太聪明的做法，我们可以先将原数组处理为其差分数组，将对原数组在区间上的修改转变成为对其差分数组的头与尾后的修改，修改完成后，对差分数组再求前缀和即可得到原数组（利用前缀和与差分互为逆运算的性质），再利用原数组去求区间和。
  • 若 $A$ 数组的差分数组为 $B$ 数组，$A[j] += x, j \in [ L_i, R_i ], j \in R$ 就等价于 $B[L_i] += x, B[R_i+1] -= x$
  • 如果 $n$ 很大怎么办？
    可以对用到的下标做离散化

扩展

异或前缀和

若 $S[1] = A[1]$，$S[i] = S[i-1] \text{ xor } A[i]$，则称 $S$ 是 $A$ 的异或前缀和，有以下性质：

$$sum[l, r] = A[l] \text{ xor } A[l + 1] \dots \text{ xor } A[r] = S[r] \text{ xor } S[l - 1]$$

二维/多维前缀和

一维前缀和扩展到二维前缀和

若 $S[i][j] = \sum\limits^{i}_{p=1}\sum\limits^{j}_{q=1} A[p][q]$，则称 $S$ 是 $A$ 的二维前缀和，多维前缀和的普通求解方法几乎都是基于容斥原理，有以下性质：

递推公式：

$$S[i][j] = S[i-1][j] + S[i][j-1] - S[i-1][j-1] + A[i][j]$$

总矩阵中的任意一个子矩阵求和（容斥原理）：

$$sum[L_1, R_1, L_2, R_2] = S[L_2][R_2] - S[L_2][R_1] - S[L_1][R_2] + S[L_1][R_1]$$

链表

定义

每个链表中的节点都包含两个值，该节点的权值和指向下一个节点的指针（或者是下一个节点的地址）

扩展

邻接链表

如果邻接矩阵来存图，用 $a[i][j]$ 表示 $i$ 与 $j$ 连边的情况，空间的大小是 $N^2$（ $N$ 为图的点数），但是要存的边数可能是很少的，譬如稀疏图，于是可能会浪费很多的空间，那么我们可以用邻接链表来优化存图

邻接链表存图的核心思想是将读入的每一条边编号，并记录下从每个点出发的第一条边的编号，并且记录下每条边的“下一条边”的编号，这样一来，当我们需要遍历从一个点出发的所有边时，只需要从该点的第一条边开始，遍历完成后找到该边的“下一条边”继续遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int cnt;
struct Edge
{
    int to;     //这条边的终点
    int next;   //这条边的下一条边
    int val;    //这条边的权值
}e[maxn];
int head[maxn]; //head[i]表示i节点的第一条边的编号

void add(int u, int v, int w)
{
    e[++cnt].to = v;
    e[cnt].val = w;
    e[cnt].next = head[u];
    head[u] = cnt;  //链表从头部插入新元素
}

栈与队列

栈

栈（stack）又名堆栈，它是一种运算受限的线性表。限定仅在表尾进行插入和删除操作的线性表。这一端被称为栈顶，相对地，把另一端称为栈底。向一个栈插入新元素又称作进栈，入栈或压栈，它是把新元素放到栈顶元素的上面，使之成为新的栈顶元素；从一个栈删除元素又称作出栈或退栈，它是把栈顶元素删除掉，使其相邻的元素成为新的栈顶元素。

性质：后进先出（last in first out）

一个手写的栈：

1
2
3
4
5
6
7
8
9
10
11
int top;
int stack[maxn];
int pop()
{
    if(top)
    return stack[top--];
}
void push(int x)
{
    stack[++top] = x;
}

C++ STL

1
2
3
4
5
6
7
#include<stack>
stack<int> s;
s.empty();      //如果栈为空则返回true，否则返回false；
s.size();       //返回栈中元素的个数
s.top();        //返回栈顶元素，但不删除该元素
s.pop();        //弹出栈顶元素，但不返回其值
s.push();       //将元素压入栈顶

括号匹配问题

例题：判断一串括号序列是否合法
思路：读取序列，若当前符号和栈顶符号匹配，则弹出栈顶，否则压入当前符号进栈

给定一个由 (、)、[、] 四种符号构成的字符串，判断其中的括号是否匹配。
如果匹配，输出 “yes”，否则输出 “no”。
Sample Input
(()()[(())])
[((]))
Sample Output
yes
no

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <bits/stdc++.h>
using namespace std;
bool check(string s);

int main() {
    string s;
    while (cin >> s) {
        if (check(s)) cout << "yes" << endl;
        else cout << "no" << endl;
    }
    return 0;
}

bool check(string s)
{
    stack<char> p;
    p.push('#');        // 设置“哨兵”，防 RE 
    for (int i = 0; i < s.size(); i++)
    {
        char c = s[i];  // string 的访问方式
        // 注意一次匹配失败即无需进行后面的判断，可以直接给出 false
        if (c == ')')
        {
            if (p.top() != '(') return false;
            else p.pop();
        } 
        else if (c == ']')
        {
            if (p.top() != '[') return false;
            else p.pop();
        } 
        else p.push(c);
    }
    return (p.size() == 1);	// 是否只剩“哨兵” 
}

排队问题

例题：

描述：有 n 个人站队，所有的人全部向右看，个子高的可以看到个子低的人发型（高个子会挡住低个子的视线，这里的身高大于是严格大于），给出每个人的身高，问所有人能看到其他人发型数量的总和是多少。
输入：4 3 7 1
输出：2
解释：个子为 4 的可以看到个子为 3 的发型（因为被 7 挡住所以看不到 1），个子为 7 可以看到个子为 1 的身高，所以 1+1 = 2
输入：3 4
输出：0
解释：3 看不到 4 的

思路：维护一个单调的栈

可以求每个人被看到的次数，即这个人向左单调递增的区间长度。

从左到右依次读取当前人的高度，从栈顶开始把高度小于或等于当前人的高度的那些元素删除，此时栈中剩下的元素的数量就是可以看见当前人的其他人的数量。

队列

队列是一种特殊的线性表，特殊之处在于它只允许在表的前端（front）进行删除操作，而在表的后端（rear）进行插入操作，和栈一样，队列是一种操作受限制的线性表。进行插入操作的端称为队尾，进行删除操作的端称为队头。

性质：先进先出（first in first out）

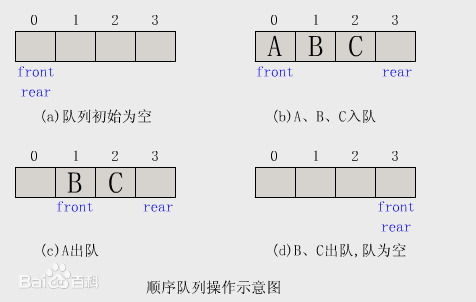
一个手写的队列：

1
2
3
4
5
6
7
8
9
10
11
int head=0, tail=0;
int q[maxn];
int pop()
{
    if(head<tail)
        return q[head++];
}
void push(int x)
{
    q[tail++]=x;
}

可以写成循环队列以优化空间复杂度

C++ STL

1
2
3
4
5
6
7
8
#include<queue>
queue<int> q;
q.empty();      // 如果队列为空返回 true，否则返回false
q.size();       // 返回队列中元素的个数
q.pop();        // 删除队列首元素但不返回其值
q.front();      // 返回队首元素的值，但不删除该元素
q.push();       // 在队尾压入新元素
q.back();       // 返回队尾元素的值，但不删除该元素

队列的 BFS 搜索

Description：定义一个二维数组：

int maze[5][5] = {
    0, 1, 0, 0, 0,
    0, 1, 0, 1, 0,
    0, 0, 0, 0, 0,
    0, 1, 1, 1, 0,
    0, 0, 0, 1, 0,
};

它表示一个迷宫，其中的 1 表示墙壁，0 表示可以走的路，只能横着走或竖着走，不能斜着走，要求编程序找出从左上角到右下角的最短路线。
Input
一个 5 x 5 的二维数组，表示一个迷宫。数据保证有唯一解。
Output
左上角到右下角的最短路径。

思路：

一道比较简单的 BFS 搜索题目，在 BFS 过程中记得记录该节点的前驱

  1. 将起点压入队列
  2. 取出队首元素 now，若 now 为终点则结束，
    否则从 now 向外扩展其他可行的点（若出界或者已经访问过或者是障碍物则不可行），
    将新点压入队列，返回第二步开始

双端队列

即在队首和队尾都支持插入和删除操作的数据结构

优先队列（堆）

优先队列中，元素被赋予优先级。当访问元素时具有最高优先级的元素最先删除。优先队列具有最高级先出（first in, largest out）的行为特征。

top 访问队头元素
empty 队列是否为空
size 返回队列内元素个数
push 插入元素到队尾（并排序）
emplace 原地构造一个元素并插入队列
pop 弹出队头元素

复杂度分析按堆来分析

1
2
3
4
// 升序队列
priority_queue <int, vector<int>, greater<int> > q;
// 降序队列
priority_queue <int, vector<int>, less<int> > q;

自己写自己的结构体：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <iostream>
#include <queue>
using namespace std;

// 方法1
struct tmp1 //运算符重载<
{
    int x;
    tmp1(int a) { x = a; }
    bool operator<(const tmp1& a) const
    {
        return x < a.x;     // 大顶堆
    }
};

// 方法2
struct tmp2 //重写仿函数
{
    bool operator() (tmp1 a, tmp1 b)
    {
        return a.x < b.x;   // 大顶堆
    }
};
    priority_queue<tmp1> d;
    priority_queue<tmp1, vector<tmp1>, tmp2> f;

例题：

两个排好序的序列A、B（长度为 n，n 为 1e5），求前 n 大的 A[i]+B[j]，分别是多少？A、B 都是降序

思路：

使用一个优先队列，一开始先将 A 序列中最大的那个和 B 序列所有元素依次相加存进队列中，每次弹出最大的和组合（$A_i, B_j, A_i + B_j$）再新加入（$A_{i+1}, B_j, A_{i+1} + B_j$）
但好像并不需要优先队列，用双指针遍历 n 次就能解决问题了