b站视频链接：北京理工大学ACM冬季培训课程
 课程刷题地址 2020BIT冬训-DFS&&BFS&&图 Password: bfshedfsnandubuda(好像并不需要)
本篇博文为看视频学习时的记录与自己的一些总结

DFS&&BFS&&图
- DFS 与 BFS
  - DFS 类枚举
    - 枚举全排列
    - 枚举集合
    - 枚举组合
  - 剪枝初探
  - 二维平面问题
    - 迷宫问题
- 图
  - 图的概念
  - 树的概念
  - 图的表示
    - 邻接矩阵
    - 邻接表
    - 邻接表的 DFS 与 BFS 操作
  - 其他

DFS&&BFS&&图

¶DFS 与 BFS

你穿越到了异世界，你想要找到这个异世界的一对儿红毛+蓝毛双胞胎女仆，但毕竟人生地不熟，你知道的信息只有：
当前你所在的位置；你所在的位置连接有几条路，以及这些路通向哪里；
现在，你想到达这张图的所有地方，请给出一种不重复的，且便于程序实现的策略。
举个栗子：你初始在 $1$ 号位置。

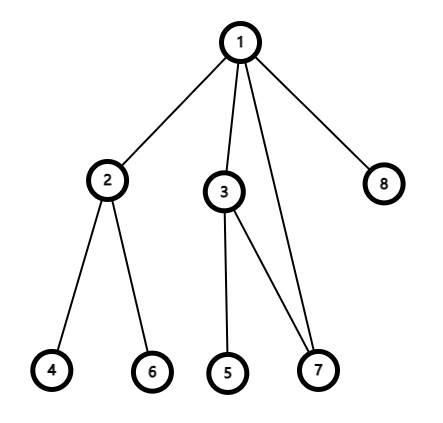
DFS：深度优先搜索——一往无前，有路就走；用递归实现

到了 (位置 P) {
    for (每个能走的位置 Q) {
        如果没到过 Q
        到了 (位置 Q)
        记录 Q 到过了
    }
    返回一步
}

DFS 序列：1 2 4 6 3 5 7 8

BFS：广度优先搜索——稳中求进，由近及远；用队列实现

重复:
    取出队首的位置 P
    for (每个能走到的位置 Q)
        Q 入队
        走到 Q 看看
        返回一步
直到队列为空

BFS 序列：1 2 3 7 8 4 6 5

DFS 与 BFS 序列都不唯一，这里假设多个选择的时候优先选数字小的

DFS 与 BFS 既是遍历图的方式，也是一种搜索思想

¶DFS 类枚举

常用到 $vis$ 数组做标记
灵活掌握递归函数的传参很重要
一般可以写成这种形式

DFS(某状态) {
    如果搜出一种结果 返回;
    在所有能做出的选择中: {
        做出该选择并记录该选择做过;
        DFS(选择后的状态);
        取消该选择以及对该选择的记录;
    }
}

¶枚举全排列

全排列的枚举：
输入 $n$，按字典序输出所有 $1$ ~ $n$ 的全排列，$n$ 不超过 $10$
例如：输入 $3$，输出 $\{ 1,2,3 \}$，$\{ 1,3,2 \}$，$\{ 2,1,3 \}$，$\{ 2,3,1 \}$，$\{ 3,1,2 \}$，$\{ 3,2,1 \}$

#include <bits/stdc++.h>
using namespace std;
int n;
vector<int> ans;

void show(){
    for (int i = 0; i < ans.size(); i++){
        printf("%5d", ans[i]);
    }putchar('\n');
    return;
} 
int vis[12];
void dfs(int num){
    if (num == n + 1){
        show();
        return;
    }
    for (int i = 1; i <= n; i++){
        if (!vis[i]){
            ans.push_back(i);
            vis[i] = 1;
            dfs(num + 1);
            ans.pop_back();
            vis[i] = 0;
        }
    }
}

int main(){
    cin >> n;
    dfs(1);
    return 0;
}

时间复杂度 $O(n!)$
next_permutation 很强大！可以生成下一个全排列并判断是否生成了所有 $n!$ 个全排列，但需要定义小于号

int main(){
    cin >> n;
    for (int i = 1; i <= n; i++){
        ans.push_back(i);
    }
    do {
        show();
    } while( next_permutation(ans.begin(), ans.end()) );
    return 0;
}

¶枚举集合

集合的枚举：
给一个 $n$ 个元素的集合，输出他的所有子集，$n$ 不超过 $10$
例如：$\{ 1,2,3 \}$ 需要输出 $\{ \}$，$\{ 1 \}$，$\{ 2 \}$，$\{ 3 \}$，$\{ 1,2 \}$，$\{ 1,3 \}$，$\{ 2,3 \}$，$\{ 1,2,3 \}$

void dfs(int num){
    if (num == n + 1){
        show();
        return;
    }
    // √
    ans.push_back(num);
    dfs(num + 1);
    ans.pop_back();
    // X 
    dfs(num + 1);
    return;
}

时间复杂度 $O(2^n)$
可以用位运算来非递归的枚举

¶枚举组合

组合的枚举：
给一个 $n$ 个元素的集合，输出从该集合中选出 $k$ 个元素的所有方案
例如：$\{ 1,2,3 \}$ 中选两个需要输出 $\{ 1,2 \}$，$\{ 1,3 \}$，$\{ 2,3 \}$

时间复杂度 $O(n^k)$
类似全排列，在 DFS 函数的判断终止条件处改一下即可

¶剪枝初探

给你一个 $9*9$ 的数独，填了它

V1.0：这不和枚举全排列差不多吗
搜索对象：所有的空位置上试着填 $1$ ~ $9$ 所有的数字
终止条件：无空位置（填满了），判断是否合法
V2.0：可行性剪枝
在 V1.0 的基础上，每填一个数字，check 一次；（不再填 $1$ ~ $9$ 所有的数字，而填当前能合法的数字）
幂小于指数，早剪早享受
搜索对象：所有的空位置上试着填合法的所有的数字
终止条件：无空位置（填满了），那就是答案了
V3.0：排除等效冗余
不用搜所有的空位置，选一个搜就可以了
搜索对象：在某一个空位置上试着填合法的所有的数字
终止条件：无空位置（填满了），那就是答案了
V4.0：搜索顺序剪枝
在所有位置中，总是选择合法数字最少的位置来填
一些搜索问题只要求我们找到一组可行解（或可行解唯一，抑或判断是否可行），所以我们争取做到不用搜完所有情况就可以出答案
搜索对象：在合法数字最少的一个空位置上试着填合法的所有数字
终止条件：无空位置（填满了），那就是答案了

¶二维平面问题

利用 $dx[\ ]$, $dy[\ ]$ 这种数组来高效地写 $4$ 方向、$6$ 方向、$8$ 方向的移动
DFS 或 BFS 可以解决一些判断联通、可达的问题；各自有各自的用处

int dx[] = { 0, 1, 0, -1 };
int dy[] = { 1, 0, -1, 0 };
...
for (int i = 0; i < 4; i++){
    xx = x + dx[i], yy = y + dy[i];
    // do something
}

有 $N*M$ 大小的农田，下雨后积水，格子中 ‘W’ 代表积水，’.’ 代表未积水的土地，每个格子被认为和相邻的 $8$ 个格子相连，一片相互连接的积水叫做 “水WA”，根据农田的航拍图确定有多少个 “水WA”

¶迷宫问题

给你个只含有障碍和平地的二维迷宫，问你两个点是否互相可达？
问两个点之间的最短距离是多少？
问题一，只要从一个点开始 BFS 看能不能到另外一个就可了
问题二，使用 dis[N][N] 数组（初始化为负无穷）记录所有点到起点之间的最短距离
每次从队列取出一点时，试着更新周围各点距离
当前点：$px$，$py$；周围一点：$xx$，$yy$；则通过这个更新：

1	dis[xx][yy] = min(dis[xx][yy], dis[px][py] + 1)

为什么 BFS 这样可以找到最短路？
距离关于入列顺序单调不减
入列顺序越靠后的一个点相对于起始点的距离一定不会短于比它在队列中位置靠前的点

¶图

¶图的概念

图 $G$ 由顶点集 $V$ 和边集 $E$ 组成，记为 $G = (V, E)$
要素：顶点（Vertex）与边（Edge）和边权（Weight）
边分为有向边和无向边

更多的概念：

顶点弧弧尾弧头有向图边无向图
完全图有向完全图稀疏图稠密图
权网子图邻接点度入度出度
路径回路（环）简单路径
连通连通图连通分量强连通图强连通分量生成树
自环重边

¶树的概念

对于 $n$ 个顶点的无向图：
满足有 $n-1$ 条边且连通，就是树（但是树可以是空树，图不可以是空图）

好的性质：
没有任何环，两点之间简单路径唯一

¶图的表示

图的存储结构：邻接矩阵，邻接表，十字链表，邻接多重表

¶邻接矩阵

对角线全为 $0$，矩阵对称（无向图）
可能需要初始化
$O(1)$ 判断两点间是否有边
炸空间，存稀疏图有大量无效元素
代码实现：二维数组

¶邻接表

每个点要存一个序列，序列长度可能不等
用 vector 实现邻接表
完全可以取代前向星
如果有边权的话，vector 的数据类型设为 pair 或者自定义的结构体 node 即可

¶邻接表的 DFS 与 BFS 操作

BFS 操作

void dfs(int now) {
    ans.push_back(now);
    vis[now] = 1;
    for (auto to : a[now]) {
        if (!vis[to]) {
            dfs(to);
        }
    }
    return;
}

BFS 操作

queue<int> q;
void bfs(int st) {
    q.push(st);
    vis[st] = 1;
    while (!q.empty()) {
        int now = q.front();
        ans.push_back(now);
        q.pop();
        for (auto to : a[now]) {
            if (!vis[to]) {
                q.push(to);
                vis[to] = 1;
            }
        }
    }
    return;
}

测试代码（包含 main 函数）

#include <bits/stdc++.h>
using namespace std;
vector<int> a[10];
vector<int> ans;
int n, m;
bool vis[12];

int main()
{
    cin >> n >> m;
    int u, v;
    for (int i = 1; i <= m; i++) {
        scanf("%d%d", &u, &v);
        a[u].push_back(v);
        a[v].push_back(u);
    }
    // dfs or bfs
    for (int i = 1; i <= n; i++) {
        printf("%d%c", ans[i-1], (i == n) ? '\n' : ' ');
    }
    for (int i = 1; i <= n; i++) {
        printf("%d%c", vis[i], (i == n) ? '\n' : ' ');
    }
    return 0;
}
/* 
测试数据：这个图就是本文开头介绍 DFS 与 BFS 用的图
8 8
1 2
1 3
1 7
1 8
2 4
2 6
3 5
3 7
*/

¶链式前向星

链式前向星（邻接表的静态数组实现）

需要初始化为 $-1$
数组从下标为 $1$ 开始用，下标为 $0$ 的空间不用
空间节省

int n,m,s,u,v,w,cnt,head[100005];
struct Edge{
    int to, dis, next;
}edge[200005];
void Add_edge(int from, int to, int w){
    edge[++cnt].to=to;
    edge[cnt].dis=w;
    edge[cnt].next=head[from];
    head[from]=cnt;
}

for(int i=1; i<=m; i++){
    scanf("%d%d%d", &u, &v, &w);
    Add_edge(u, v, w);
}

遍历图的所有的边：

for(int i=1; i<=n; i++)
{
    // 每个内循环访问第 i 个顶点出发的所有边
    for(k=head[i];~k;k=edge[k].next)
    {
        // 得到了 k 值，就可以到 edge 中找到对应边
        // 然后这里就可以做具体的处理过程
    }
}

¶其他

DFS 序：
随便选个点 DFS，全过程中依次到达的点的编号组成的序列（同一个点出现一次 or 两次）

树的直径：
树上距离最远的两点，可以通过两次 BFS 求解
先找到树的一个叶结点，一次 BFS 找到一个离该结点最远的一个点 $A$，再以 $A$ 为起始点 BFS 找到离 $A$ 最远的点 $B$，$A$、$B$ 的距离即为树的直径

树的重心：
以该点作为根时，各个子树中点数最多的子树点数最少

关于 DFS 与 BFS 推荐阅读：dfs和bfs