LeetCode Day8
链表
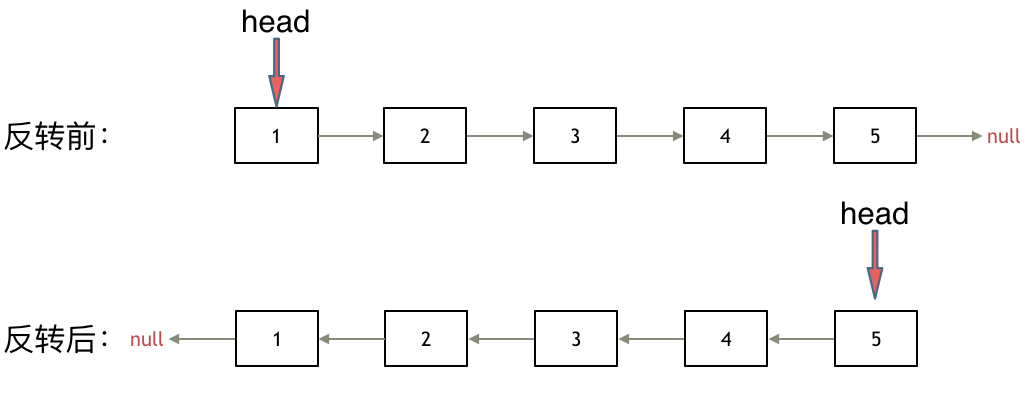
翻转链表
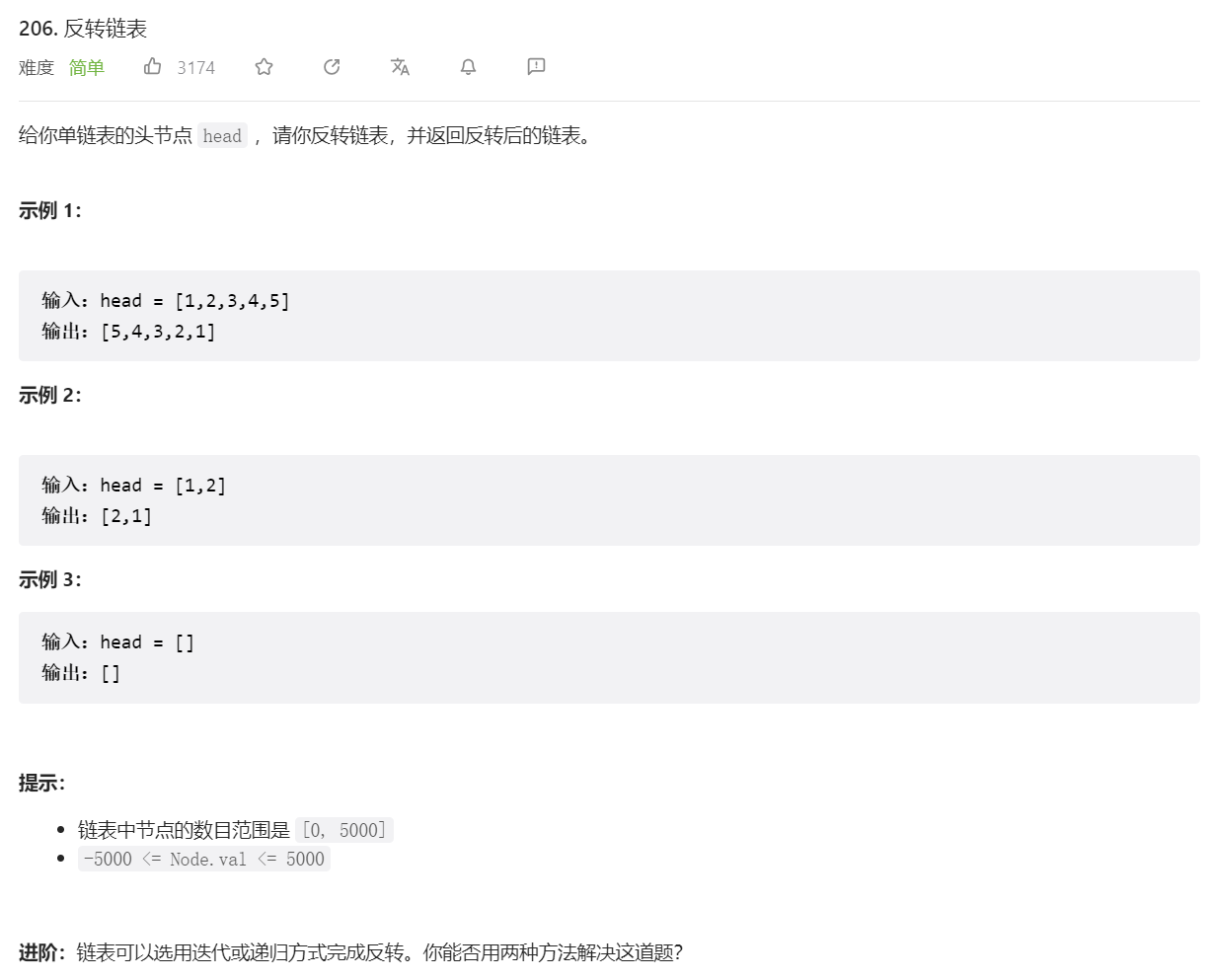
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
class Solution {
public:
ListNode* reverseList(ListNode* head) {
if (head == NULL) return head;
ListNode* dummyHead = new ListNode(0, head);
ListNode* tail = dummyHead->next;
ListNode* temp;
while (tail->next != NULL) {
temp = tail->next;
tail->next = temp->next;
temp->next = dummyHead->next;
dummyHead->next = temp;
}
head = dummyHead->next;
return head;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
|
ListNode* reverseList(ListNode* head) {
ListNode* cur = head;
ListNode* pre = nullptr;
ListNode* temp;
while (cur != NULL) {
temp = cur->next;
cur->next = pre;
pre = cur;
cur = temp;
}
head = pre; return head;
}
ListNode* reverse(ListNode* pre,ListNode* cur){
if(cur == NULL) return pre;
ListNode* temp = cur->next;
cur->next = pre;
return reverse(cur,temp);
}
ListNode* reverseList(ListNode* head) {
return reverse(NULL, head);
}
ListNode* reverseList(ListNode* head) {
if(head == NULL) return NULL;
if (head->next == NULL) return head;
ListNode *last = reverseList(head->next);
head->next->next = head;
head->next = NULL;
return last;
}
|
两两交换链表中的节点
.PNG)
.PNG)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
class Solution {
public:
ListNode* swapPairs(ListNode* head) {
ListNode* dummyHead = new ListNode(0, head);
ListNode* pre, * cur1, * cur2;
pre = dummyHead;
while (pre->next != nullptr && pre->next->next != nullptr) {
cur1 = pre->next;
cur2 = cur1->next;
pre->next = cur2;
cur1->next = cur2->next;
cur2->next = cur1;
pre = cur1;
}
head = dummyHead->next;
return head;
}
};
|
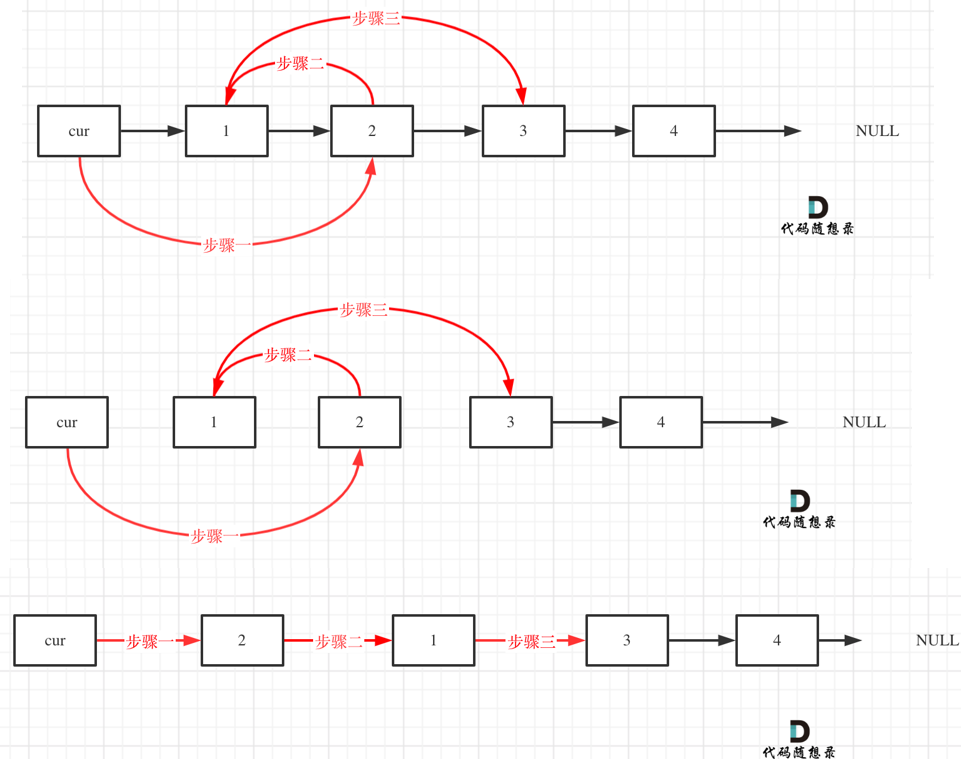
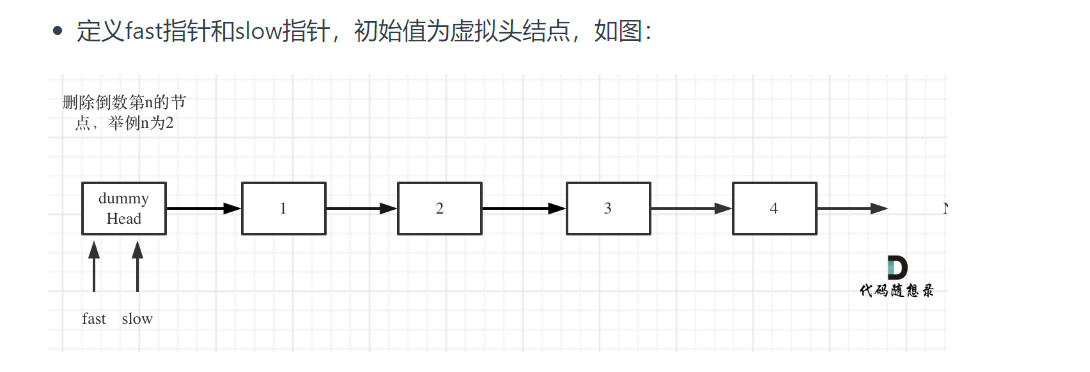
删除链表的倒数第N个节点
.PNG)
.PNG)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
class Solution {
public:
static int cnt;
void removeNode(ListNode* pre) {
ListNode* temp = pre->next;
pre->next = pre->next->next;
delete(temp);
}
void findN(ListNode* node) {
if (node == nullptr) return;
findN(node->next);
if (!(cnt--)) removeNode(node);
}
ListNode* removeNthFromEnd(ListNode* head, int n) {
cnt = n;
ListNode* dummyHead = new ListNode(0, head);
ListNode* cur = dummyHead;
findN(cur);
head = dummyHead->next;
return head;
}
};
int Solution::cnt = 0;
|
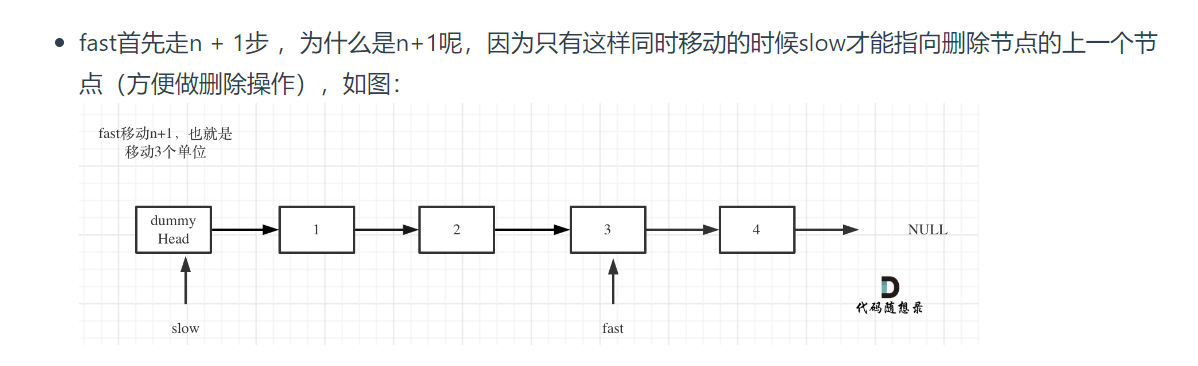
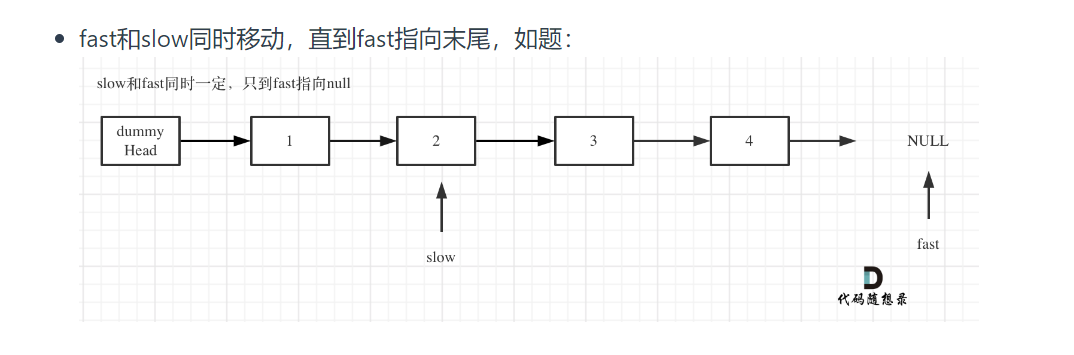
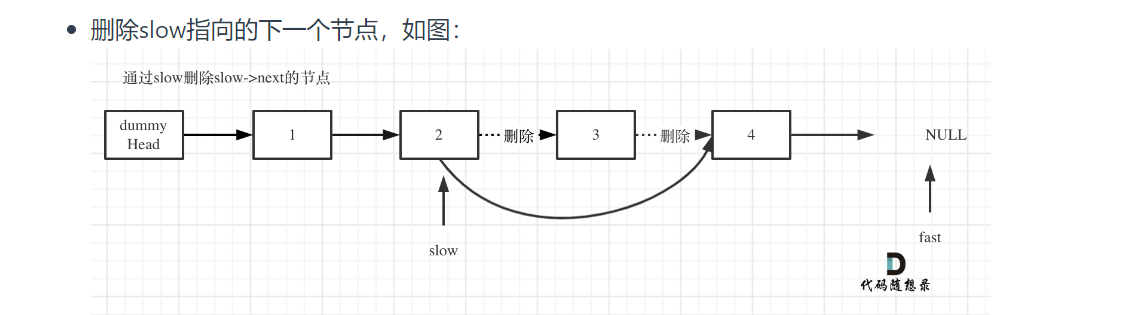
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode* fastIndex, * slowIndex;
ListNode* dummyHead = new ListNode(0, head);
fastIndex = dummyHead; slowIndex = dummyHead;
while (n--) { fastIndex = fastIndex->next; }
while (fastIndex->next != NULL) {
fastIndex = fastIndex->next;
slowIndex = slowIndex->next;
}
ListNode* temp = slowIndex->next;
slowIndex->next = slowIndex->next->next;
delete(temp);
head = dummyHead->next;
return head;
}
};
|
相交链表
.PNG)
.PNG)
.PNG)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
ListNode* IntersectionNode = NULL;
ListNode* dummyHeadA = new ListNode(0);
dummyHeadA->next = headA;
ListNode* dummyHeadB = new ListNode(0);
dummyHeadB->next = headB;
ListNode* indexA = dummyHeadA, * indexB = dummyHeadB;
int sizeA = 0, sizeB = 0;
while (indexA->next != nullptr) { sizeA++; indexA = indexA->next; }
while (indexB->next != nullptr) { sizeB++; indexB = indexB->next; }
indexA = dummyHeadA, indexB = dummyHeadB;
int n = abs(sizeA - sizeB);
if (sizeA > sizeB) while (n--) { indexA = indexA->next; }
if (sizeA < sizeB) while (n--) { indexB = indexB->next; }
while (indexA != nullptr && indexB != nullptr) {
if (indexA == indexB) {
IntersectionNode = indexA;
break;
}
indexA = indexA->next, indexB = indexB->next;
}
return IntersectionNode;
}
};
|
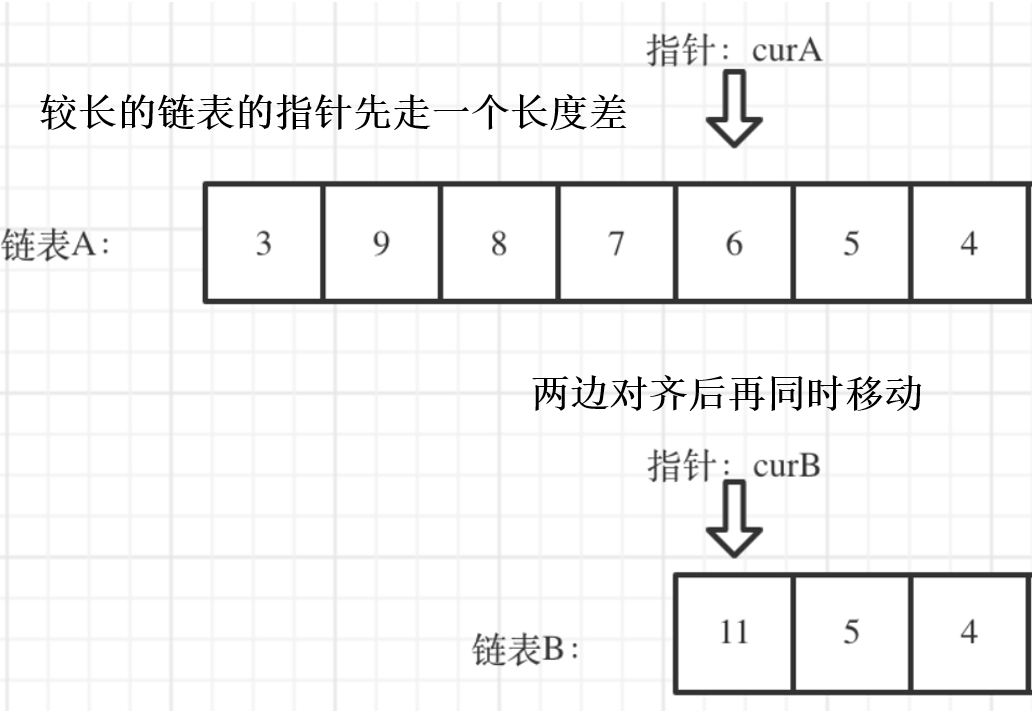
环形链表
.PNG)
.PNG)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
|
class Solution {
public:
ListNode* detectCycle(ListNode* head) {
ListNode* firstnodeofcycle = NULL;
ListNode* fast = head, * slow = head;
while (fast != NULL && fast->next != NULL) {
slow = slow->next;
fast = fast->next->next;
if (slow == fast) {
ListNode* index1 = fast;
ListNode* index2 = head;
while (index1 != index2) {
index1 = index1->next;
index2 = index2->next;
}
firstnodeofcycle = index1;
return firstnodeofcycle;
}
}
return firstnodeofcycle;
}
};
void printCycle(ListNode* head) {
ListNode* firstNodeOfCycle = detectCycle(head);
if (firstNodeOfCycle == NULL) { printf("No Cycle\n"); return; }
ListNode* temp = firstNodeOfCycle;
do
{
printf("%d ", temp->val);
temp = temp->next;
} while (temp != firstNodeOfCycle);
printf("\n");
}
int main() {
ListNode* node_1 = new ListNode(-4);
ListNode* node_2 = new ListNode(0, node_1);
ListNode* node_3 = new ListNode(2, node_2);
ListNode* head = new ListNode(3, node_3);
node_1->next = node_3;
printCycle(head);
return 0;
}
|
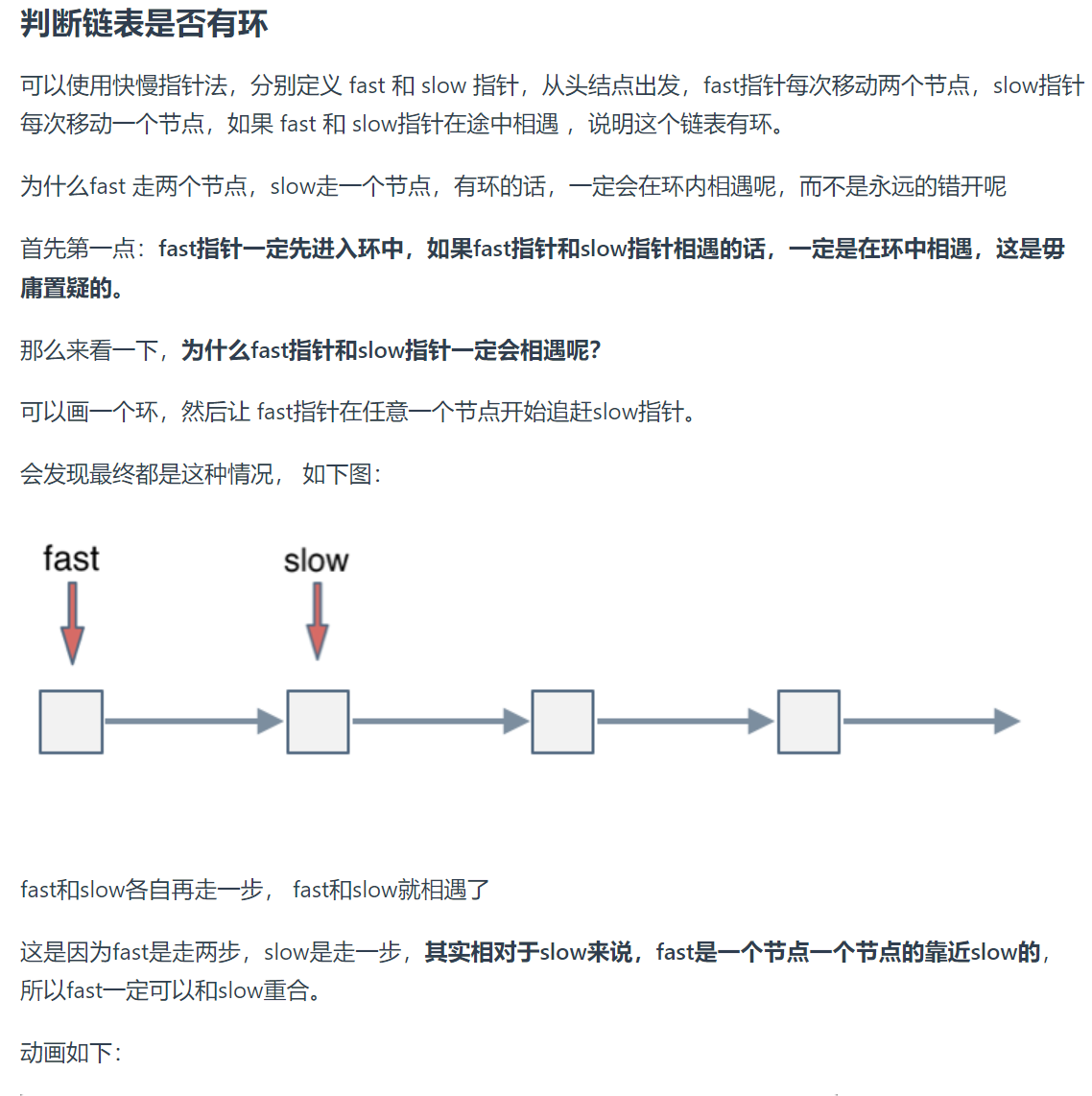
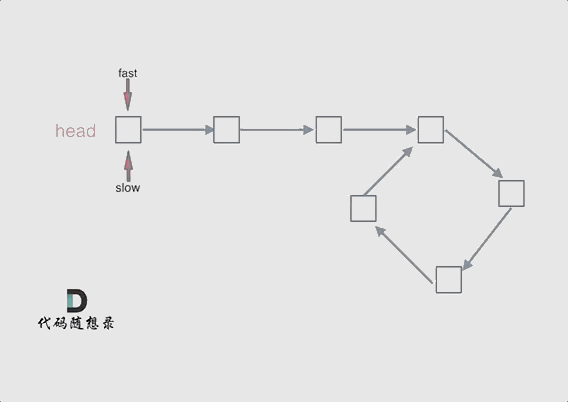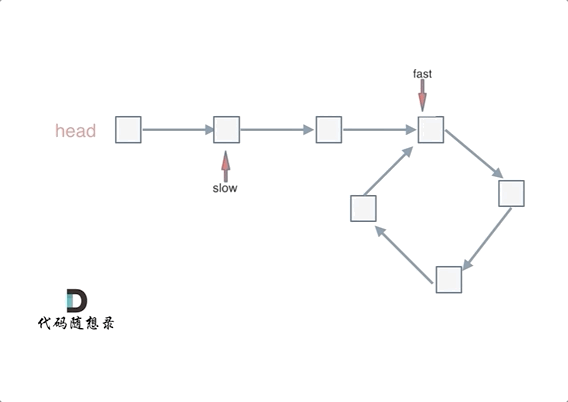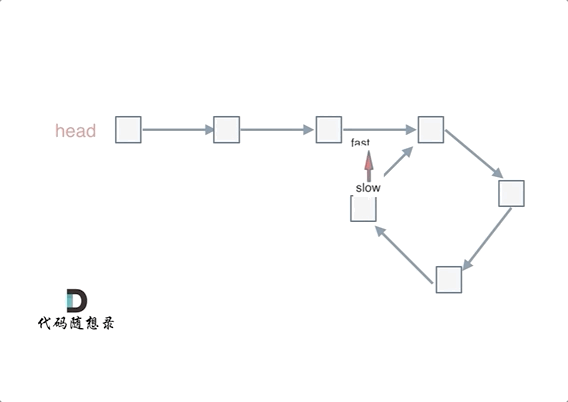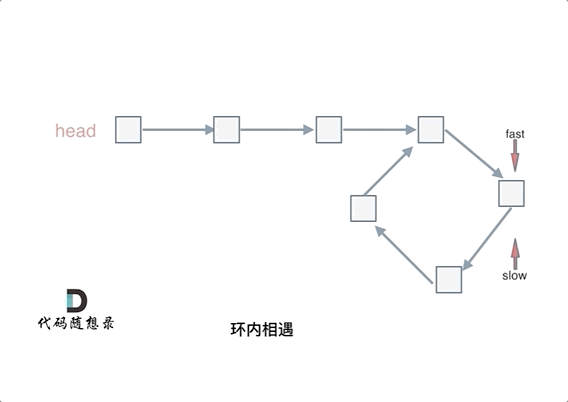

补充:为什么第一次在环中相遇,slow的 步数 是 x + y 而不是 x + 若干环的长度 + y
总结
.PNG)
个人总结
.PNG)
来自代码随想录



