课本:《理论力学(I)》(第六版) 哈尔滨工业大学理论力学教研室 编
¶绪论
一、任务
研究物体机械运动一般规律的科学
一般规律 -> 特殊规律:
陀螺:定向性 | 地震时房屋桥梁的震动:机械振动
一般规律:最一般最普遍、一般工程中最常遇到
为了研究问题的方便,将理论力学分为三部分:
静力学:研究物体受力分析,力系等效替换,建立各种力系的平衡条件的科学
运动学:研究物体机械运动几何性质的科学
动力学:研究物体机械运动几何性质与作用力之间关系的科学
二、研究方法
从实践到理论、从理论到实践,循环往复、不断上升
抽象:质点、刚体
分类法
三、目的
- 直接解决工程实际问题
- 为后继课程打基础
四、特点
理论易懂、掌握困难
¶静力学
¶静力学引言
一、任务
二、基本概念
- 力:物体之间的相互机械作用,使得物体的机械运动状态发生变化
(什么作用都可以,不一定加 “机械” 两个字) - 力的三要素:大小、方向、作用点
书写:$\boldsymbol F$ 或 $\vec F$
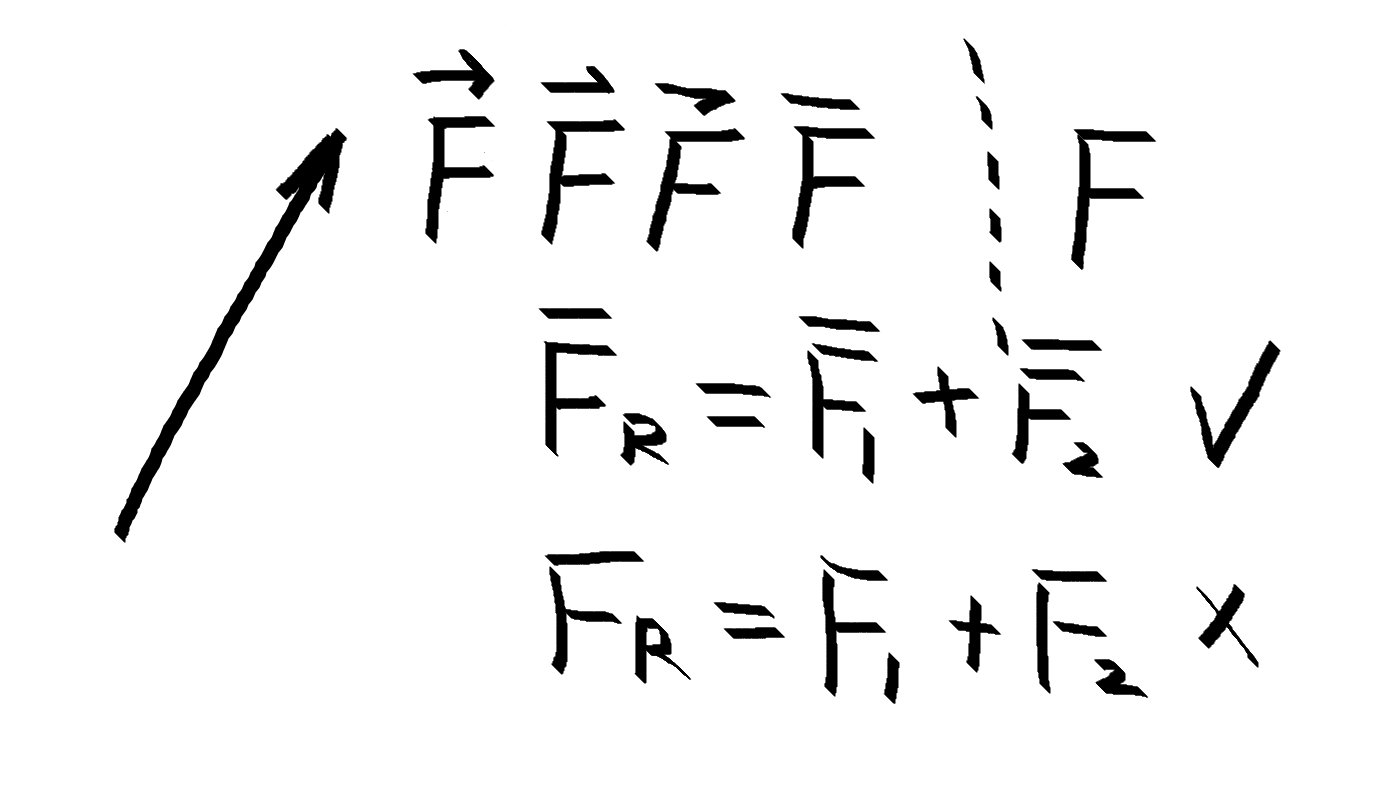
- 力系:共点力系、汇交力系、平行力系、任意力系;平面力系、空间力系;力偶系;共线力系;
- 刚体和变形体:相对的
- 力的可传性:对刚体成立,对变形体不成立
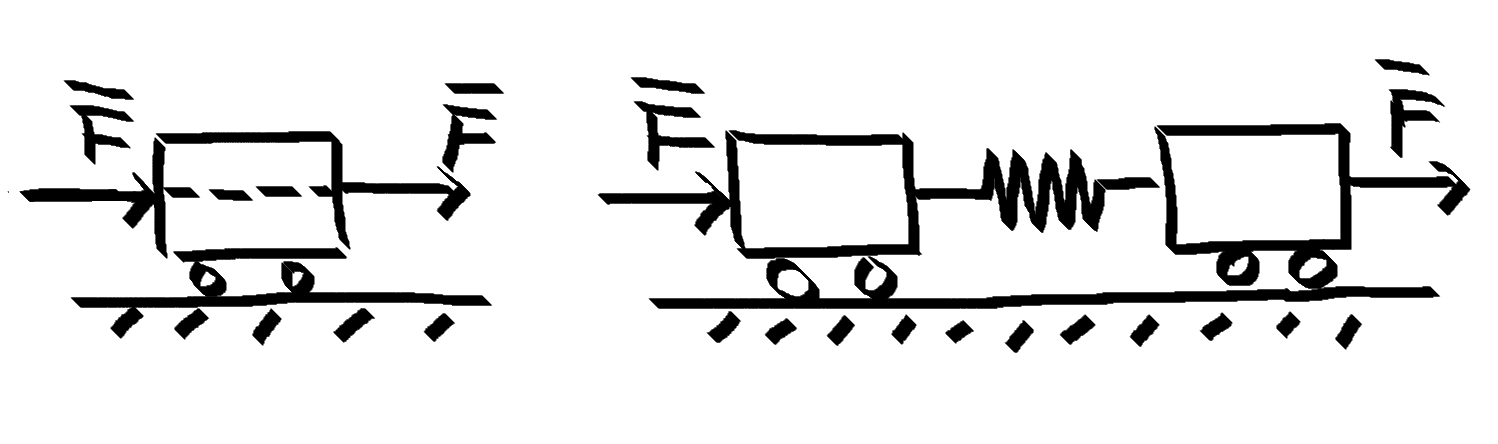
- 平衡:物体相对地面静止,或者作匀速直线运动
¶静力学公理和物体的受力分析
¶$\S\ 1-1$ 静力学公理
一、二力平衡公理
作用在刚体上的两个力,使刚体保持平衡的必要和充分条件是:这两个力的大小相等,方向相反,且作用在同一直线上
二、加减平衡力系公理
在已知力系上加上或减去任意的平衡力系,并不改变原力系对刚体的作用
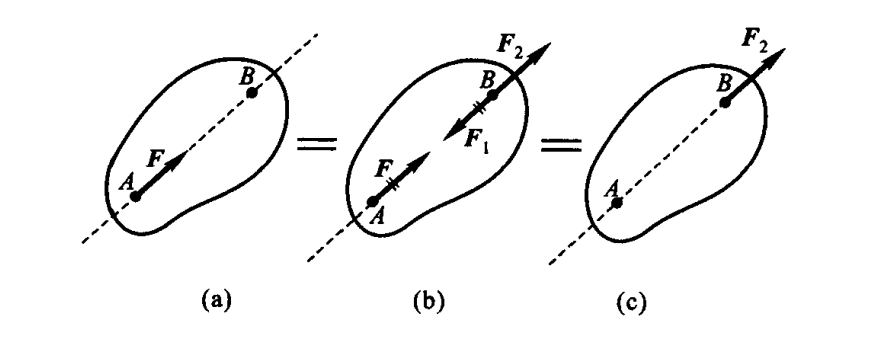
推论一:力的可传性
作用于刚体上某点的力,可以沿着它的作用线移到刚体内任意一点,并不改变该力对刚体的作用
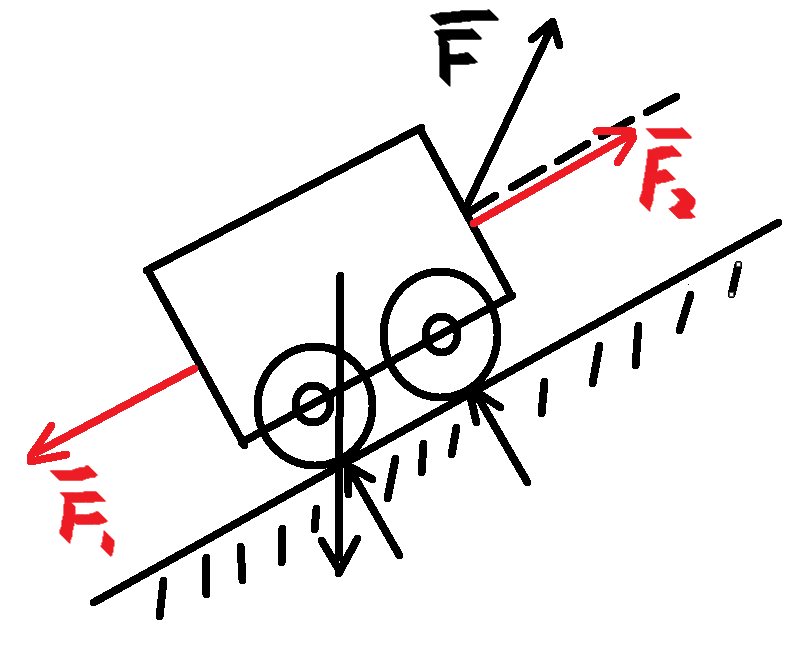
三、平行四边行公理(法则)
$$\boldsymbol F_R = \boldsymbol F_1 + \boldsymbol F_2$$
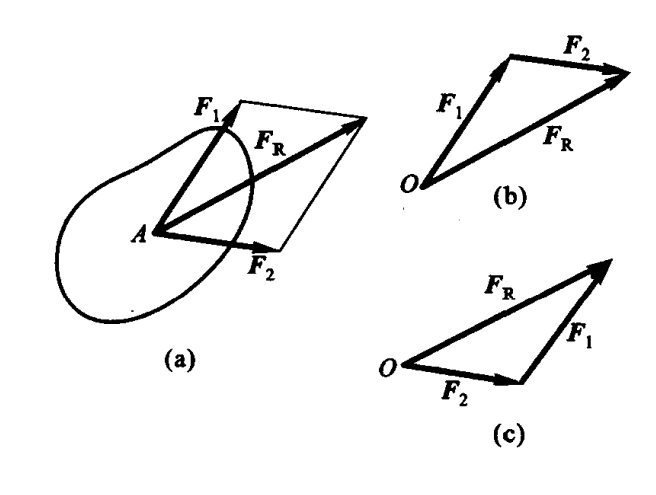
推论二:三力平衡汇交定理
一个刚体在三个力的作用下平衡,有两个力的作用线已经交于一点,第三个力能不能作用在任意位置?
推导:力的可传性 $\rightarrow$ 平行四边形法则 $\rightarrow$ 二力平衡公理
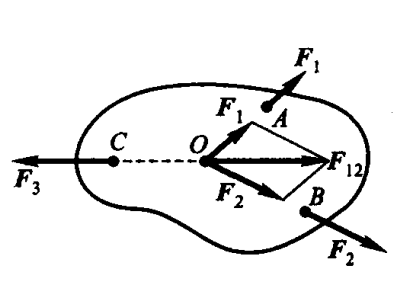
第三个力的作用线必须通过汇交点,且三个力在同一平面内
四、作用反作用公理(定律)
作用力与反作用力:大小相等、方向相反,沿着同一直线,分别作用在两个相互作用的物体上
$$\boldsymbol F = - \boldsymbol F’$$
五、刚化公理
变形体在某一力系作用下处于平衡,如将此变形体刚化为刚体,其平衡状态保持不变
¶$\S\ 1-2$ 约束和约束力
约束:限制物体位移的物体
约束力:约束给被约束物体的力,约束力的方向必与该约束所能够阻碍的位移方向相反
约束分类:
一、光滑(面、线、点)接触约束
阻碍物体沿接触表面法线并向约束内部的位移
作用在接触点处,方向沿接触表面的公法线并指向被约束的物体(法向约束力)
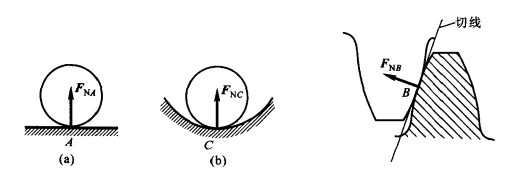
二、柔性体(各种绳索、皮带、链条等)约束
约束力只可能是拉力
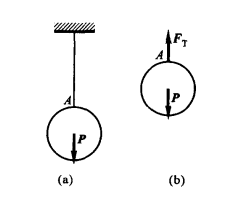
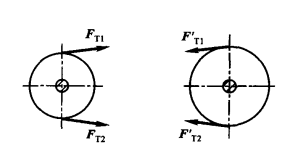
三、光滑铰链(径向轴承、圆柱型销钉、固定铰支座等)约束
向心轴承(径向轴承)
主动力未确定,接触点不能确定,约束力的方向不能确定
但约束力的作用线必垂直于轴线并通过轴心,可用通过轴心的两个正交分力 $\boldsymbol F_{Ax}$,$\boldsymbol F_{Ay}$ 表示
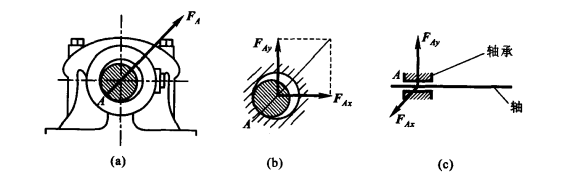
圆柱型销钉(圆柱铰链)(太抽象了,想想剪刀)
圆柱铰链,即由销钉将两个钻有同样大小孔的构件连接在一起而成
固定铰支座,即铰链连接中有一个固定在地面或机架上作为支座
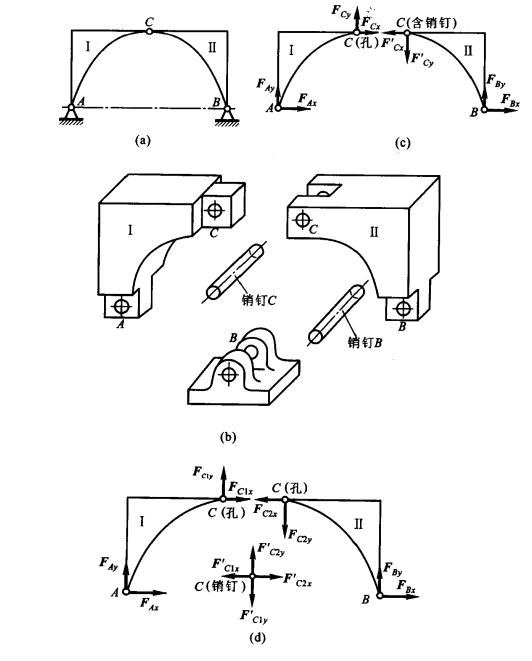
径向轴承、圆柱型销钉、固定铰支座,这三种约束的具体结构不同
但构成约束的性质是相同的,都可以表示为光滑铰链
特点是:只限制两物体径向的相对移动,而不限制两物体铰链中心的相对转动及沿轴向的位移
四、其他分类
(1)可(滚)动铰支座
在固定铰链支座与光滑支承面之间装有辊轴,约束性质与光滑面约束相同
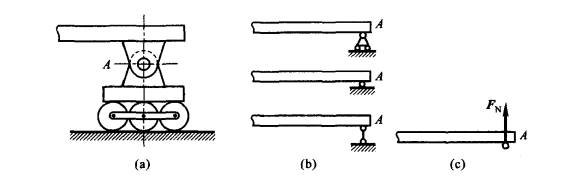
(2)球铰链
通过圆球与球壳将两个构件连接在一起的约束
构件的球心不能有位移,但构件可绕球心任意转动
其约束力是一个通过接触点与球心,方向不能预先确定的空间法向约束力
可用三个正交分力 $\boldsymbol F_{Ax}$,$\boldsymbol F_{Ay}$,$\boldsymbol F_{Az}$
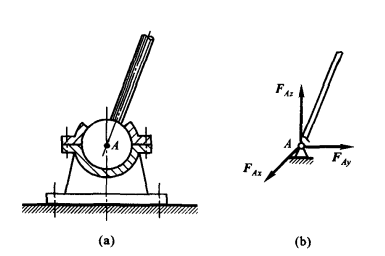
(3)止推轴承
与径向轴承相比,不仅限制轴的径向位移,还限制轴沿轴向的位移
即多了一个沿轴向的约束力,即有三个正交分量 $\boldsymbol F_{Ax}$,$\boldsymbol F_{Ay}$,$\boldsymbol F_{Az}$
实际工程应用

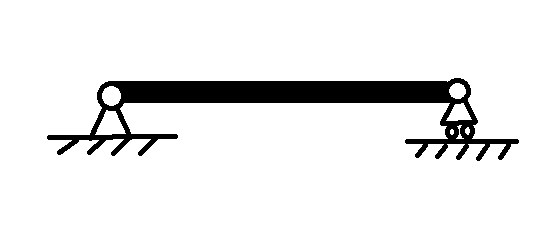

¶$\S\ 1-3$ 物体的受力分析和受力图
受力分析 | 主动力 | 被动力 | 受力体 | 施力体 | 取研究对象 / 取分离体 | 受力图
步骤通常为:
- 取研究对象 / 取分离体,画出简图
- 画出所有主动力
- 依据约束性质画出所有约束力(不画内力)
一个例子:
有这样一个平面三角构架,A、C 点均用固定铰支座连接到垂直平面,B 点以圆柱型销钉连接 AB 与 BC 杆,对 AB、BC 两杆作受力分析,并画出受力图(具体工程应用:老式火车行李架)
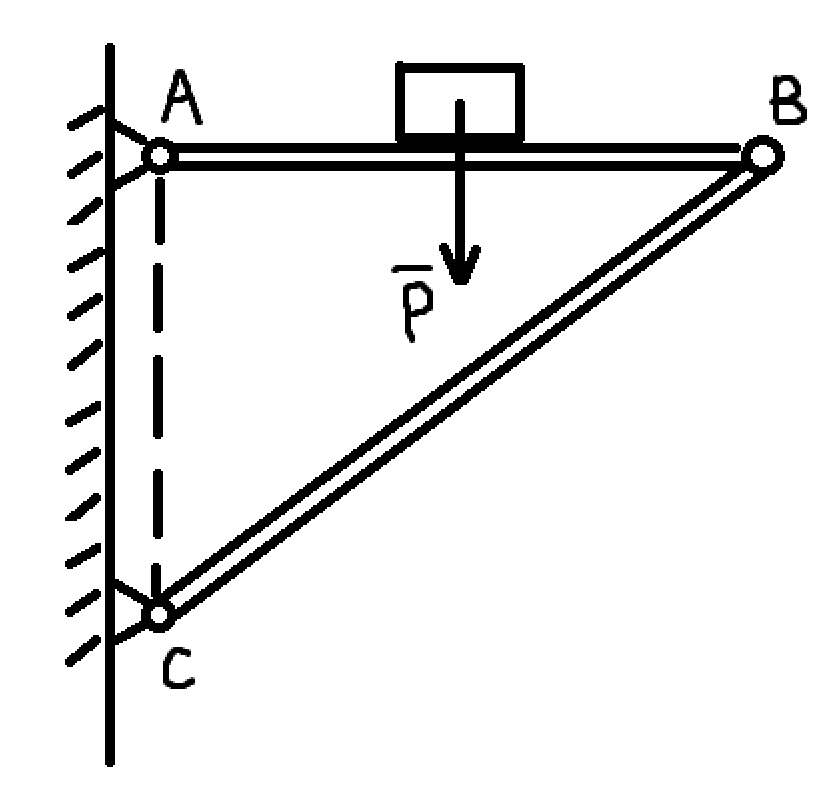
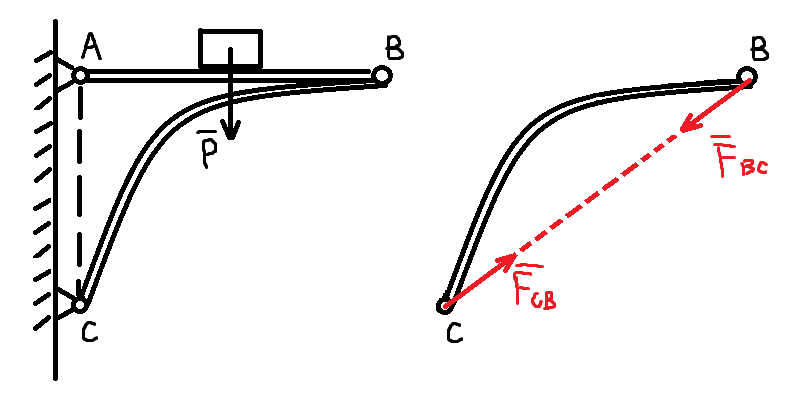
为了研究 AB、BC 杆的受力情况,我们将其分离出来,这有个说法,叫取分(隔)离体,AB 杆上物体受重力 $\boldsymbol P$,AB 杆自重为 $\boldsymbol P_1$,这一类力为主动力,一般是已知的,如物体的重力、风力、气体压力
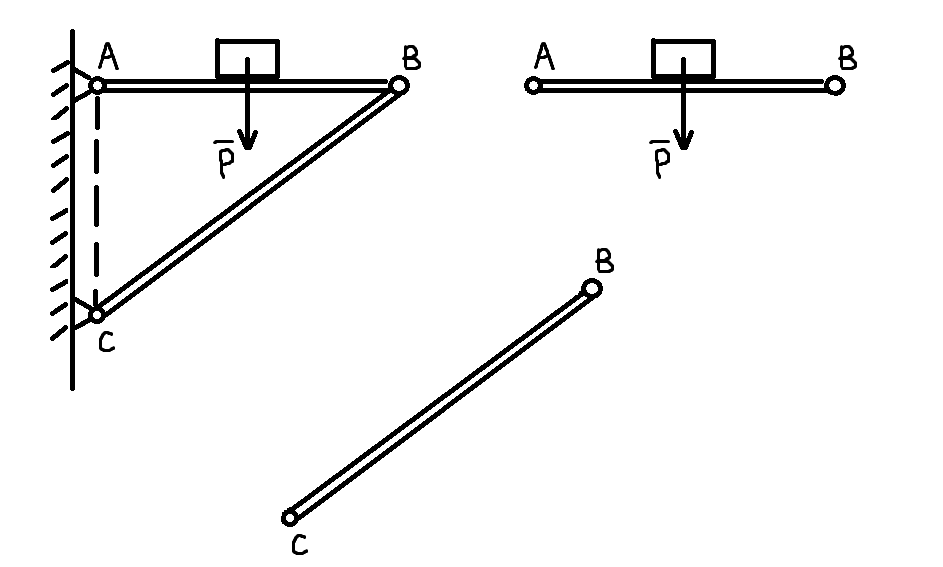
对水平杆分析受力,方向均不能确定,用两个正交分量来表示,由受力图可知,$\boldsymbol F_{Ax}$ 与 $\boldsymbol F_{Bx}$ 必为一正一负
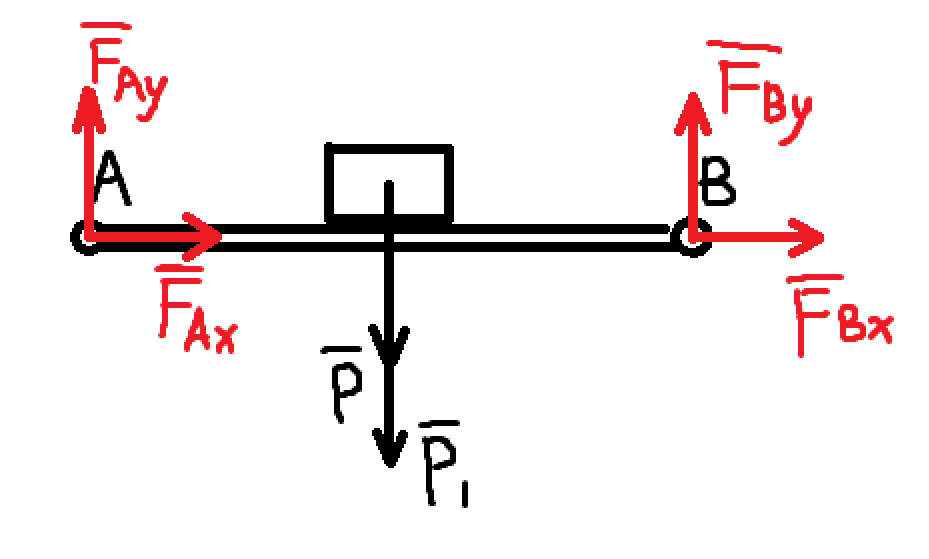
由作用反作用公理,B 点的受力可以表示,C 点受的力方向不能确定,也用两个正交分量来表示
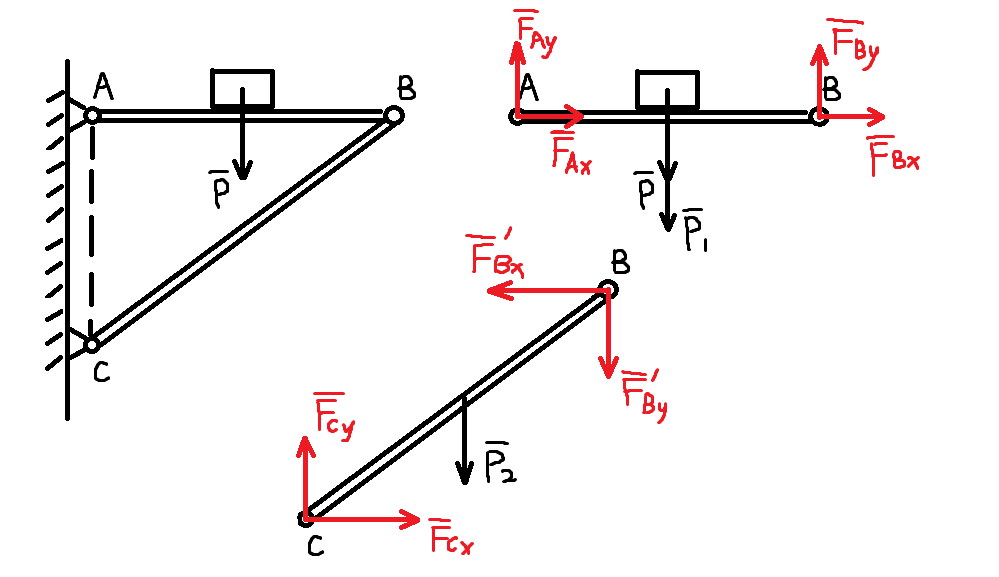
上图只能算一个 “质量不好” 的受力图,什么是好的呢?
(我们先加一个条件不计(忽略)杆的自重)
我们看到,BC 杆实质上是在两个力的作用下平衡,作用点分别在 B、C 点,由二力平衡公理,这两个力必定沿同一直线,且等值反向,作用线是确定的,即沿 B、C 的连线,可见 BC 杆就是受压力的
这里有一个新名词,这样的杆件叫做 “二力杆”,如果是构件的话,就叫 “二力构件”,即只在两个力作用下平衡的构件,二力构件的受力特点是,两个力必定沿着两个力作用点的连线,且大小相等,方向相反
判断二力构件的依据就是二力平衡公理,做题经常用上
由作用反作用公理,可以确定水平杆中 B 点的受力情况,再由三力平衡汇交定理,A 点处的受力情况也可确定
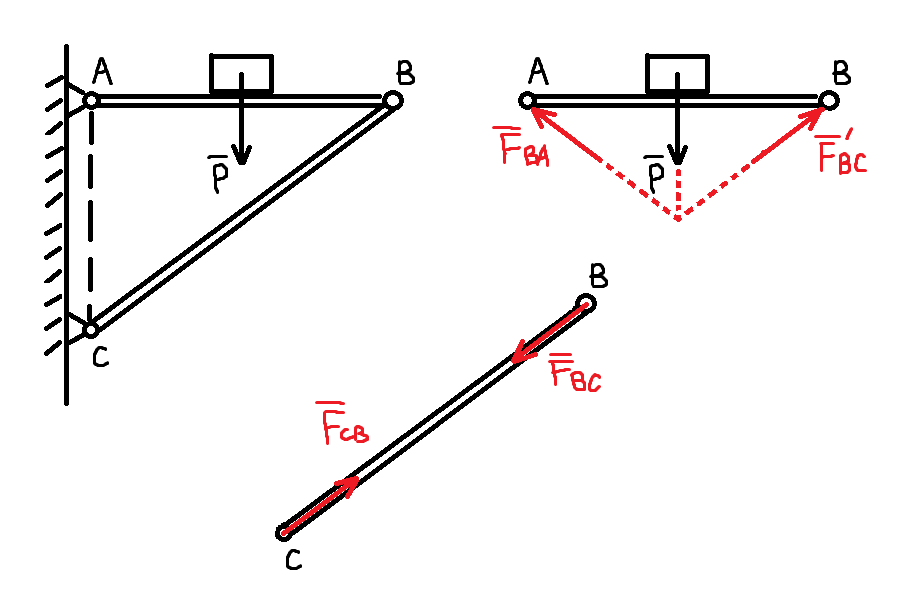
为了美观和节省空间,这里的斜杆通常是弧形杆,做受力分析,发现它还是二力杆,所以的话,二力杆与杆件形状没有关系,仅与其受力有关
又一个例子:
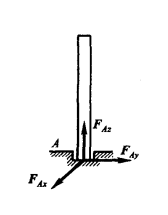
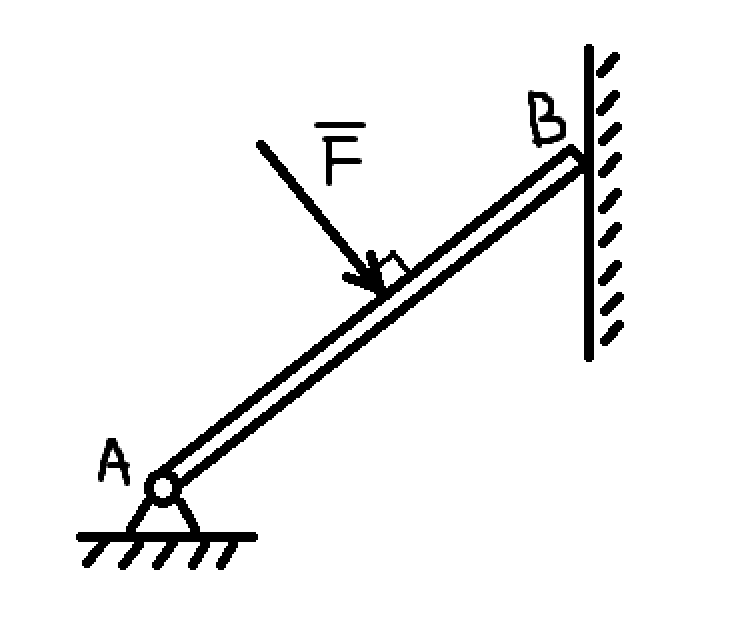
AB 杆受到一个垂直的作用力 $\boldsymbol F$,A 点以固定铰支座连接到地面,B 点与垂直于地面的光滑墙面接触,对 AB 杆作受力分析,并画出受力图
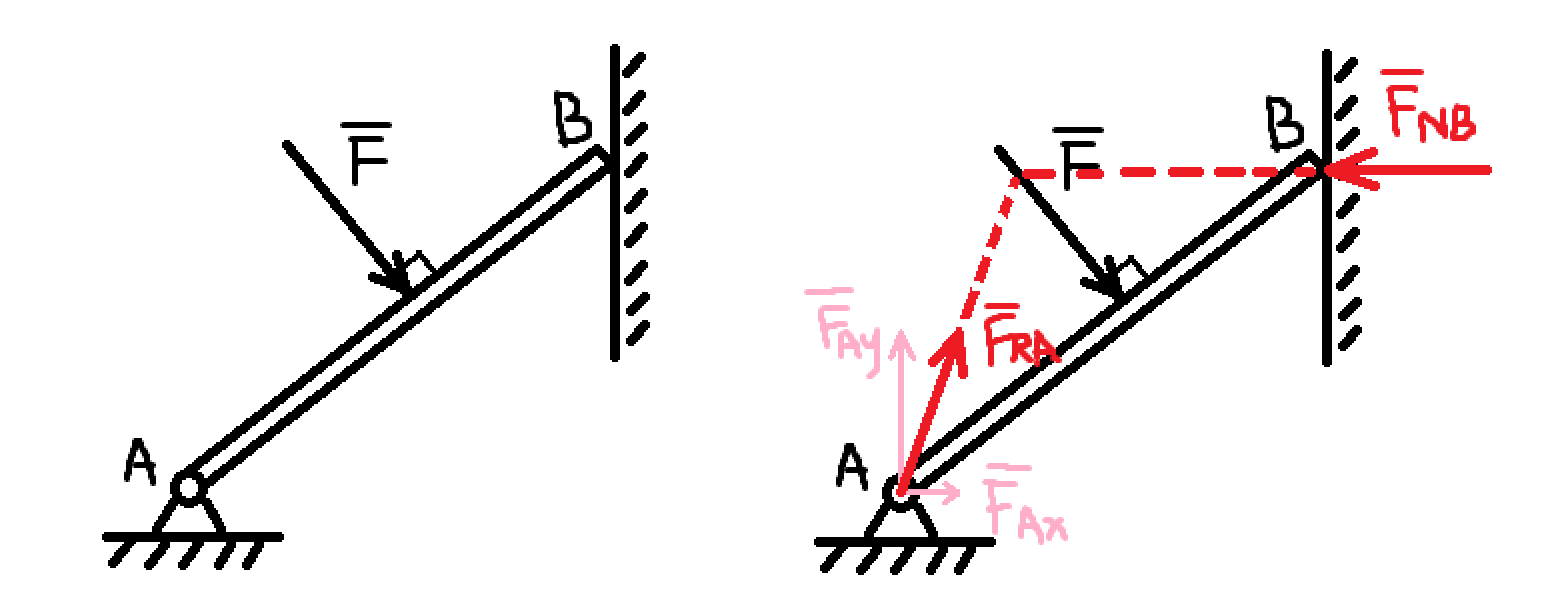
容易出错的是,误将墙面的支持力方向判断为垂直于 AB 杆向上,若是这样,将这个力分解,既有水平分力又有竖直分力,墙面光滑,可能产生竖直分力的摩擦力不会有,只可能有水平方向上的力
正确的分析步骤:
由于是光滑接触约束,约束力作用在接触点处,方向沿接触表面的公法线并指向被约束的物体,将该力记为 $\boldsymbol F_{NB}$,如图所示;A 点处对杆的作用力(记为 $\boldsymbol F_{RA}$)可以表示为两个正交分力 $\boldsymbol F_{Ax}$ 与 $\boldsymbol F_{Ay}$,也可由三力平衡汇交定理判断出 $\boldsymbol F_{RA}$ 的方向(用不用三力平衡汇交定理因题而异)
¶$\S\ 1-4$ 力学模型和力学简图(补充)
力学建模:将实际问题抽象为力学模型的过程
力学建模的原则
- 抓住关键、本质因素、忽略次要因素
- 多方面进行抽象化处理
在实际问题的处理中,通常
- 将非均匀材料假设成均匀
- 将结构有变形的抽象成刚体
- 将三维物体处理成二维
- 将复杂形状简化为简单形状
- 将载荷简化为集中力或分布力
- 将很多约束简化为理想约束
力学简图:将力学模型用简单明了的图形来表示
一个力学简图可能对应多种实际结构,一个实际结构也可能简化成不同的力学模型
¶平面汇交力系与平面力偶系
¶$\S\ 2-1$ 平面汇交力系合成与平衡的几何法
汇交力系:
各力的作用线都汇交于一点的力系。可分为空间汇交力系和平面汇交力系
合力:
多个力汇交于一点,如果能用一个力来等效替换,此力称为合力
如果一个力与某一力系等效,则称此力为该力系的合力
(1)两个共点力的合成:力三角形规则
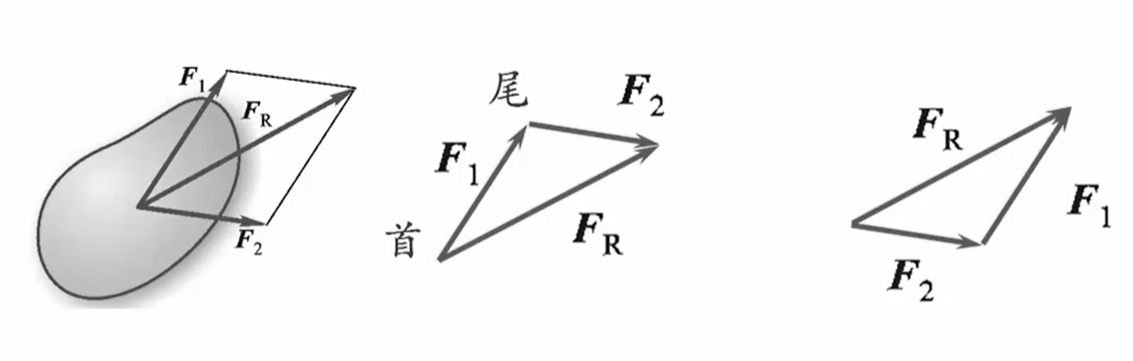
注意:力三角形规则求出的是合力的大小和方向,作用点仍在交汇点
(2)多个汇交力的合成:力多边形规则
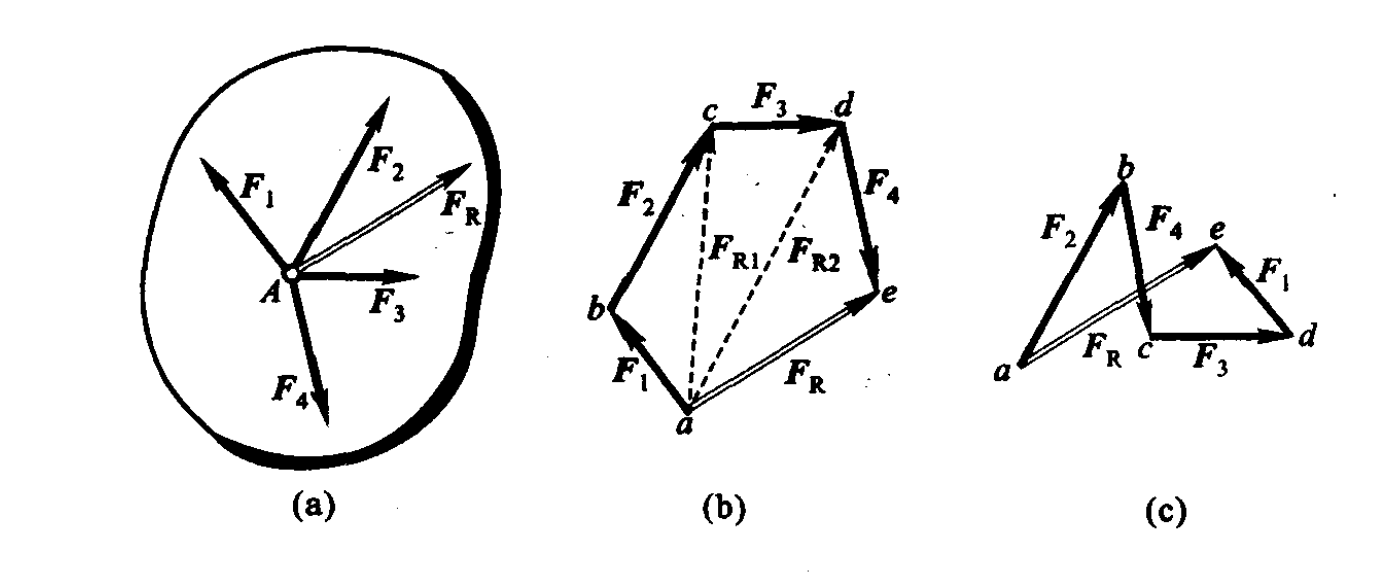
$$\boldsymbol F_{R1} = \boldsymbol F_1 + \boldsymbol F_2$$
$$\boldsymbol F_{R2} = \sum_{i=1}^{n} \boldsymbol F_i = \boldsymbol F_{R1}+ \boldsymbol F_3$$
$$…$$
$$\boldsymbol F_{R} = \boldsymbol F_1 + \boldsymbol F_2 + \cdots + \boldsymbol F_n = \sum_{i=1}^{n} \boldsymbol F_i$$
注意:力多边形规则求出的是合力的大小和方向,作用点仍在交汇点
(3)汇交力系平衡的几何条件
平面汇交力系平衡的必要和充分条件是:该力系的合力等于零,即
$$\sum_{i=1}^{n} \boldsymbol F_i = \boldsymbol 0$$
在平衡情形下,力多边形中最后一力的终点与第一力的起点重合,此时的力多边形称为封闭的力多边形,可知,平面汇交力系平衡的必要和充分条件是:该力系的力多边形自行封闭,这是平衡的几何条件
力多边形规则求合力和平衡的几何条件适用于任意汇交力系
这里是一个例子:
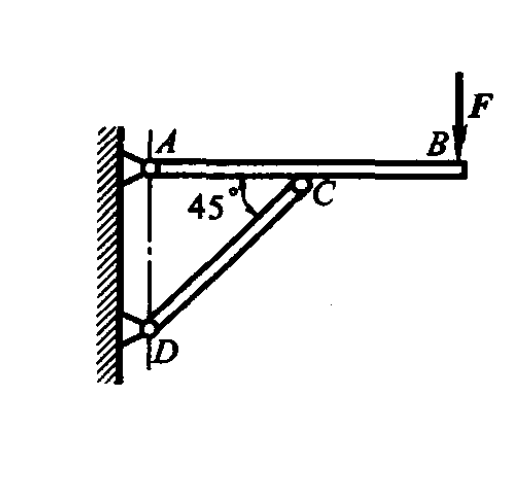
支架的横梁 AB 与斜杆 DC 彼此以铰链 C 相联接,并各以铰链 A,D 连接于铅直墙上,如图所示
已知 AC = CB,杆 DC 与水平线成 45 度角,载荷 $F = 10 \ \text{kN}$,作用于 B 点。设梁和杆的重量忽略不计,求铰链 A 的约束力和杆 DC 所受的力
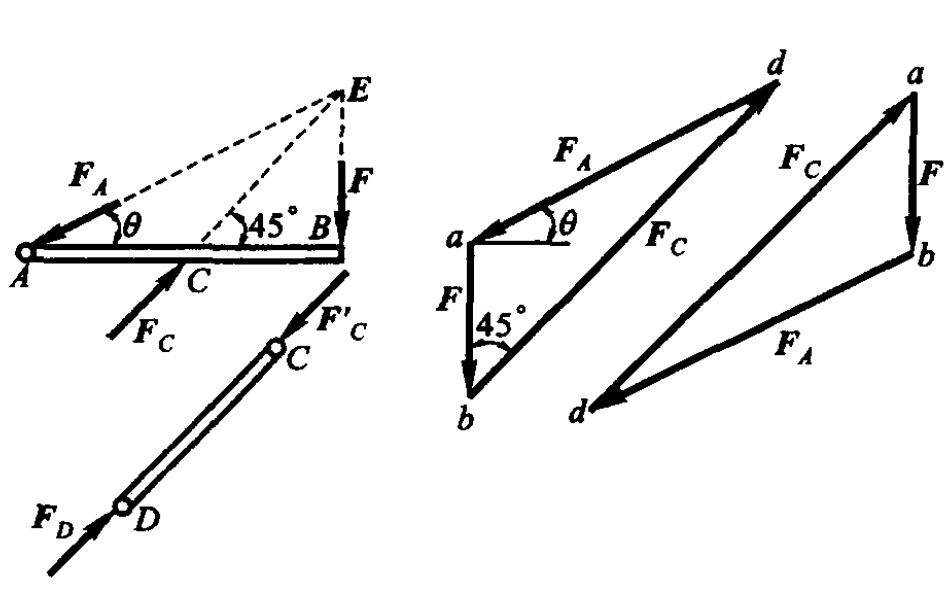
DC 为二力杆,受压,取横梁 AB 为研究对象,横梁在 B 处受载荷 $\boldsymbol F$ 作用,在 C 处受反作用力,在 A 处受铰链 A 的约束力 $\boldsymbol F_A$,可由三力平衡汇交定理确定
汇交力系,利用平衡的几何条件,画封闭的力三角形
根据三角函数计算($\tan\theta = \dfrac{1}{2}$)可知
$$\boldsymbol F_C = 28.3 \ \text{kN}\ \ \ \ \boldsymbol F_A = 22.4 \ \text{kN}$$
¶$\S\ 2-2$ 平面汇交力系合成与平衡的解析法
(1)力在直角坐标系上的投影和力沿轴的分解

力 $\boldsymbol F$ 在这个平面直角坐标系中向 x 轴上投影,得到它在 x 轴上的大小 $F_x$
显然,$F_x = F\cos\theta$,类似的,我们可以得到力 $\boldsymbol F$ 在 y 轴上的投影 $F_y = F\sin\theta$
由力的平行四边形法则,我们知道可以将力 $\boldsymbol F$ 表示成 $F_x$ 和 $F_y$ 的矢量和,即
$$\boldsymbol F = \boldsymbol F_x + \boldsymbol F_y = F_x \boldsymbol i + F_y \boldsymbol j$$
其中,$F_x$,$F_y$ 即为 $\boldsymbol F$ 在 x 轴和 y 轴上的分量的大小,等于 $\boldsymbol F$ 在两个坐标轴上的投影,这就是力沿直角坐标轴的分解
力在坐标轴上的投影一般不等于力沿着该坐标轴的分解,但是直角坐标系下二者是相等的,所以一般的静力学问题大多选择在直角坐标系下进行分析
(2)平面汇交力系合成的解析法
$$\boldsymbol F_R = \sum \boldsymbol F_i$$
由合矢量投影定理:合矢量在某一轴上的投影等于各分矢量在同一轴上投影的代数和,得合力投影定理:
$$F_{Rx} = \sum F_{ix}\ \ \ \ F_{Ry} = \sum F_{iy}$$
合力的大小为:
$$F_R = \sqrt{{F_{Rx}}^2 + {F_{Ry}}^2}$$方向为:
$$\cos(\boldsymbol F_R, \boldsymbol i) = \dfrac{\sum F_{ix}}{F_R} \ \ \ \ \cos(\boldsymbol F_R, \boldsymbol j) = \dfrac{\sum F_{iy}}{F_R}$$作用点为力的汇交点
(3)平面汇交力系平衡的解析条件(平衡方程)
由 $\S 2-1$ 可知,平面汇交力系平衡的必要和充分条件是:该力系的合力 $\boldsymbol F_R$ 等于零,即
$$F_R = \sum \boldsymbol F_i = \sqrt{(\sum F_{ix})^2+(\sum F_{iy})^2} = 0$$欲使上式成立,必须同时满足
$$\sum F_{ix} = 0 \ \ \ \ \sum F_{iy} = 0$$
这就是平面汇交力系的平衡方程,即平面汇交力系平衡的必要和充分条件是:各力在两个坐标轴上投影的代数和分别等于零

